ВЕЛИЧИНЫ.
Цель: Ввести биноминальный закон распределения, закон распределения Пуассона, законы распределения непрерывных случайных величин, свойства функций распределения и плотности (для функции распределения чередуя случаи дискретной и непрерывной случайных величин). Вывести формулу попадания случайной величины в интервал.
Ключевые слова: Биномиальный закон распределения,распределения Пуассона,
равномерное, показательное распределение, нормальный закон распределения, кривая Гаусса, функция Лапласа, мода, медиана, правило «трех сигм ».
План лекции:
1. Биномиальное распределения
2. Закон распределения Пуассона.
3. Равномерное, показательное распределение.
4. Нормальный закон распределения.
1. Биномиальный закон распределения.
Биномиальным называют закон распределения дискретной случайной величины 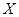 - числа появлений события в
- числа появлений события в 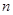 независимых испытаниях, в каждом из которых вероятность появления события равна
независимых испытаниях, в каждом из которых вероятность появления события равна 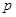 ; вероятность возможного значения
; вероятность возможного значения 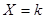 (числа
(числа 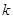 появлений события) вычисляют по формуле Бернулли:
появлений события) вычисляют по формуле Бернулли:
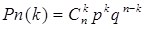
2. Закон распределения Пуассона .
Дискретная случайная величина 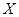 имеет распределение Пуассона, если она принимает счетное число значений: 0, 1, 2,…..,
имеет распределение Пуассона, если она принимает счетное число значений: 0, 1, 2,….., 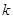 ,… с соответствующими вероятностями
,… с соответствующими вероятностями
P k = 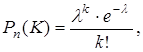
3. Равномерное, показательное распределения.
Равномерным называется такое распределение вероятностей непрерывной случайной величины Х, если на интервале (а, в), которому принадлежат все возможные значения Х, дифференциальная функция сохраняет постоянное значение, а именно 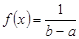 ; вне этого интервала
; вне этого интервала 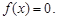
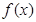
Таким образом: 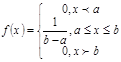
Непрерывная случайная величина 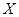 имеет показательный закон распределения с параметром
имеет показательный закон распределения с параметром 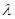 , если ее плотность вероятности имеет вид:
, если ее плотность вероятности имеет вид:
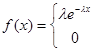
Функция распределения случайной величины 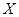 , имеющей показательный закон распределения, равна:
, имеющей показательный закон распределения, равна:
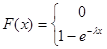
ее математическое ожидание 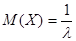 , дисперсия:
, дисперсия: 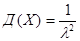
4. Нормальный закон распределения.
Нормальным называют распределение вероятностей непрерывной случайной величины 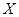 , которое описывается плотностью
, которое описывается плотностью 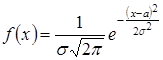 , где
, где 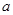 - математическое ожидание;
- математическое ожидание; 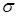 - среднее квадратическое отклонение случайной величины
- среднее квадратическое отклонение случайной величины 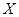 .
.
 2015-02-27
2015-02-27 465
465








