Вероятностный смысл плотности распределения

Функция 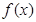определяет плотность распределения вероятности для каждой точки .

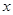Из дифференциального исчисления известно, что приращение функции приближенно равно дифференциалу функции, т.е.

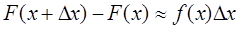
Вероятностный смысл этого равенства таков; вероятность того, что случайная величина примет значение, принадлежащее интервалу 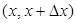приближенно равна произведению плотности вероятности в точке 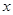на длину интервала .

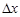4. Числовые характеристики непрерывных случайных величин

Математическим ожиданием непрерывной случайной величины 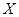, возможные значения которой принадлежат отрезку, возможные значения которой принадлежат отрезку [a,b], называют определенный интеграл

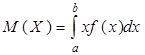
Если возможные значения принадлежат всей оси 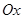, то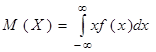

Дисперсия непрерывной случайной величины.

Дисперсией непрерывной случайной величины 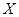называют математическое ожидание квадрата ее отклонения.

Если возможные значения 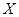принадлежат отрезку 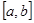, то

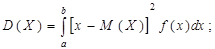
если возможные значения принадлежат всей оси х, то

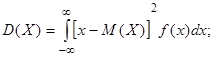
Для вычислений более удобны формулы:

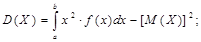
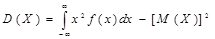
Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством .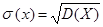

Замечание 1. Свойства математического ожидания и дисперсии дискретных случайных величин сохраняются и для непрерывных случайных величин.