Отыскание левосторонней и двусторонней критических областей

Отыскание левосторонней и двусторонней критических областей сводится к нахождению соответствующих критических точек.

Левосторонняя критическая области определяется неравенством 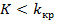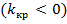. Критическую точку находят исходя из требования, чтобы при справедливости нулевой гипотезы вероятность того, что критерий примет значение, меньшее 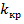, была равна принятому уровню значимости:

.

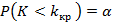Двусторонняя критическая область определяется неравенствами 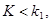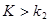. Критические точки находят исходя из требования, чтобы при справедливости нулевой гипотезы сумма вероятностей того, что критерий примет значение, меньшее 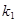или большее 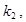была равна принятому уровню значимости:

(*)

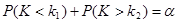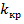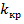
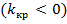Ясно, что критические точки могут быть выбраны бесчисленным множеством способов. Если же распределение критерия симметрично относительно нуля и имеются основания (например, для увеличения мощности*⁾) выбрать симметричные относительно нуля точки - и , то

.

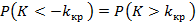Учитывая (*), получим

.

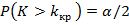Это соотношение и служит для отыскания критических точек двусторонней критической области.

2. Сравнение двух дисперсий нормальных генеральных совокупностей

На практике задача сравнения дисперсий возникает, если требуется сравнить точность приборов, инструментов, самих методов измерений и т. д. Очевидно, предпочтительнее тот прибор, инструмент и метод, который обеспечивает наименьшее рассеяние результатов измерений, т. е. наименьшую дисперсию.

Пусть генеральные совокупности X и Y распределены нормально. По независимым выборкам объемов 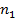и , и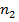звлеченным из этих совокупностей, найдены исправленные выборочные дисперси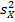и и 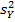. Требуется по исправленным дисперсиям, при заданном уровне значимости 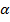, проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

.

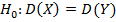Учитывая, что исправленные дисперсии являются несмещенными оценками генеральных дисперсий, т. е.

,

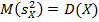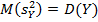
нулевую гипотезу можно записать так:

.

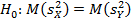Таким образом, требуется проверить, что математические ожидания исправленных выборочных дисперсий равны между собой. Такая задача ставится потому, что обычно
исправленные дисперсии оказываются различными. Возникает вопрос: значимо (существенно) или незначимо, различаются исправленные дисперсии?

Если окажется, что нулевая гипотеза справедлива, т. е. генеральные дисперсии одинаковы, то различие исправленных дисперсий незначимо и объясняется случайными причинами, в частности, случайным отбором объектов выборки. Например, если различие исправленных выборочных дисперсий результатов измерений, выполненных двумя приборами, оказалось незначимым, то приборы имеют одинаковую точность.

Если нулевая гипотеза будет отвергнута, т. е. генеральные дисперсии неодинаковы, то различие исправленных дисперсий значимо и не может быть объяснено случайными
причинами, а является следствием того, что сами генеральные дисперсии различны. Например, если различие исправленных выборочных дисперсий результатов измерений,
произведенных двумя приборами, оказалось значимым, то точность приборов различна.

В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий, примем отношение большей исправленной дисперсии к меньшей, т. е. случайную
величину

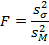
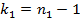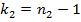Величина F, при условии справедливости нулевой гипотезы имеет распределение Фишера—Снедекора со степенями свободы и , где
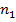- объем выборки, по которой вычислена большая исправленная дисперсия, 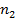- объем выборки, по которойнайдена меньшая дисперсия.

Напомним, что распределение Фишера—Снедекора зависит только от чисел степеней свободы и не зависит отдругих параметров.

Критическая область строится в зависимости от вида конкурирующей гипотезы.

Первый случай. Нулевая гипотеза .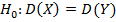

Конкурирующая гипотеза .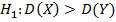

В этом случае строят одностороннюю, а именно правостороннюю, критическую область, исходя из требования, чтобы вероятность попадания критерия F в эту область,
в предположении справедливости нулевой гипотезы, была равна принятому уровню значимости:

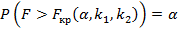
Критическую точку 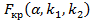находят по таблице
критических точек распределения Фишера—Снедекора (приложение 7) и тогда правосторонняя критическая область определяется неравенством

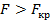
а область принятия нулевой гипотезы неравенством

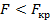
Обозначим отношение большей исправленной дисперсии к меньшей, вычисленное по данным наблюдений, через 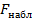и сформулируем правило проверки нулевой гипотезы.

Правило I. Для того чтобы, при заданном уровне значимости, проверить нулевую гипотезу 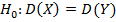о равенстве генеральных дисперсий нормальных совокупностей, при конкурирующей гипотезе: 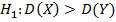,надо вычислить отношение большей исправленной дисперсии к меньшей, т. е.

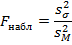
и по таблице критических точек распределения Фишера -Снедекора, по заданному уровню значимости 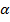и числам степеней свободы 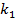и 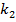(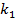,—число степеней свободы
большей исправленной дисперсии), найти критическую точку .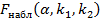

Если 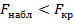- нет оснований отвергнуть нулевую гипотезу.

Если 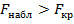- нулевую гипотезу отвергают.

3. Критерии проверки гипотез. Критерий Пирсона.

Для проверки статистических гипотез применяют критерии согласия, т.е. правила, позволяющие принять или отвергнуть выдвинутую гипотезу. Так как нормальное распределение встречается довольно часто, то наиболее часто проверяют гипотезу о соответствии выборочного распределения нормальному. Из множества критериев согласия о распределениях наиболее мощным является критерий c² Пирсона (критерий «хu-квадрат» Пирсона).

Пусть в результате 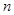наблюдений получено статистическое распределение выборки:

			…
			…

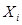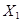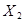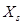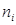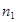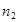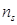Выдвинем статистическую гипотезу: «Генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение».

Критерий Пирсона представляет собой следующее правило:

Для того, чтобы проверить гипотезу о нормальном распределении генеральной совокупности, необходимо:

1. Вычислить выборочную среднюю 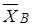и выборочное среднее квадратическое отклонение ;

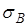2. Вычислить теоретические частоты 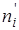формуле: ,

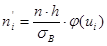где 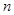-объем выборки,

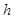- шаг (разность между двумя соседними равноотстоящими вариантами),

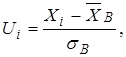
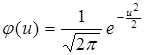(находят по таблице - приложение 1)

3. Вычислить наблюдаемое значение критерия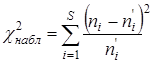

4. Вычислить число степеней свободы 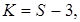где S - число групп, на которые разбита выборка;

5. Выбрать уровень значимости ;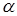

6. По таблице критических точек распределения 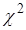найти критическую точку

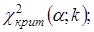
7. Если 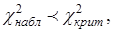, то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности, т.е. эмпирические и теоретические частоты различаются незначимо (случайно).

8. Если 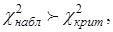то гипотезу о нормальном распределении генеральной совокупности отвергают, т.е. эмпирические и теоретические частоты различаются значимо.