Для изучения основных свойств статистического распределения используют выборочные числовые характеристики. Для нахождения центра распределения вычисляют различные типы средних величин, моду и медиану, степени вариации - размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации и другие величины.
1. Выборочная средняя арифметическая:
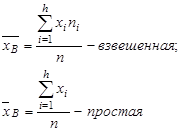 (1)
(1)
2. Выборочная средняя квадратическая:
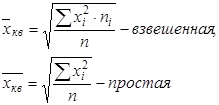 (2)
(2)
3. Выборочная средняя геометрическая:
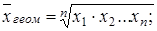 (3)
(3)
При вычислении различных типов средних величин для одного и того же вариационного ряда всегда имеем
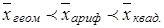
Эти неравенства характеризуют свойство мажорантности средних.
Для упрощения вычисления выборочной средней арифметической удобно переходить от данных вариант 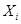 к условным вариантам
к условным вариантам 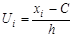 , где
, где 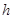 - разность между соседними вариантами,
- разность между соседними вариантами, 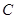 - ложный нуль (варианта с наибольшей частотой):
- ложный нуль (варианта с наибольшей частотой): 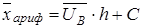 (4)
(4)
4. Модой М0 называется варианта, имеющая наибольшую частоту.
5. Медианой Ме называется такая варианта, которая делит вариационный ряд распределения на две равные части, т.е. варианта, находящаяся в середине ряда распределения.
Если в дискретном вариационном ряду 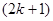 значений, то
значений, то 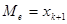 .
.
Если число вариант четное 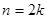 , то медиана определяется как среднее арифметическое из двух серединных значений, т.е.
, то медиана определяется как среднее арифметическое из двух серединных значений, т.е. 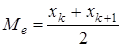 .
.
6. Размах вариации 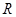 определяется как разность между максимальным и минимальным вариантами, т.е.
определяется как разность между максимальным и минимальным вариантами, т.е.
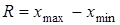 . (5)
. (5)
7. Среднее линейное отклонение – это средняя арифметическая из абсолютных значений отклонений вариант от средней арифметической
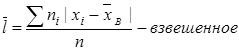 (6)
(6)
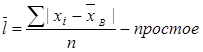
8. Дисперсией называется средний квадрат отклонения всех значений признака от его средней величины.
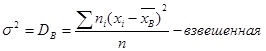 (7)
(7)
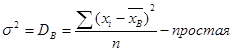
9. Исправленная дисперсия 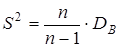 (8)
(8)
10. Среднее квадратическое отклонение равно квадратному корню из дисперсии:
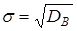 (9)
(9)
Цель: Показать смысл смещенности и несмещенности оценок, состоятельности выборочного среднего как оценки математического ожидания, выборочной дисперсии. Вести понятие асимптотически несмещенной оценки. Применять эти данные при решении задач.
Ключевые слова: Смещенные и несмещенные оценки параметров, интервальная оценка, выборочная дисперсия, доверительная вероятность, доверительный интервал.
План лекции:
1. Смещенные и несмещенные оценки параметров.
2. Точечные оценки. Метод моментов.
3. Интервальные оценки параметров.
5. Доверительный интервал.
1. Смещенные и несмещенные оценки параметров
Пусть распределение случайной величины 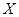 (генеральной совокупности) задается вероятностями
(генеральной совокупности) задается вероятностями 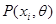 (для дискретной случайной величины) или плотностью вероятности
(для дискретной случайной величины) или плотностью вероятности 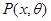 (для непрерывной случайной величины), которые зависят от неизвестного параметра
(для непрерывной случайной величины), которые зависят от неизвестного параметра 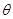 . Этим параметром может быть, например, параметр
. Этим параметром может быть, например, параметр 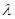 закона Пуассона или параметры
закона Пуассона или параметры 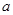 и
и 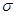 нормального распределения. На практике о величине параметра
нормального распределения. На практике о величине параметра 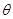 можно судить по выборке
можно судить по выборке 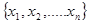 объема
объема 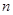 из генеральной совокупности.
из генеральной совокупности.
Оценкой 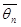 параметра
параметра 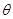 называется любая функция от значений выборки
называется любая функция от значений выборки 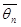 =
= 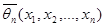 , т.е. статистика.
, т.е. статистика.
Заметим, что сам параметр 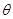 является некоторым постоянным (неслучайным) числом, которое представляет истинное значение параметра генеральной совокупности. Статистику
является некоторым постоянным (неслучайным) числом, которое представляет истинное значение параметра генеральной совокупности. Статистику 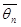 можно рассматривать как функцию от случайных величин Х1, Х2,,…, Хn , таких, что хi есть реализация случайной величины Хi:
можно рассматривать как функцию от случайных величин Х1, Х2,,…, Хn , таких, что хi есть реализация случайной величины Хi:
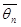 =
= 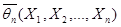
Ясно, что статистику 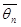 следует выбирать таким образом, чтобы ее значения как можно точнее оценивали значение неизвестного параметра
следует выбирать таким образом, чтобы ее значения как можно точнее оценивали значение неизвестного параметра 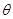 .
.
Оценка 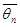 называется несмещенной, если
называется несмещенной, если 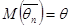 .
.
Если это требование не выполняется, то в среднем оценка 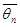 будет всегда давать значение
будет всегда давать значение 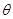 с некоторым отклонением. Для несмещенных оценок устраняется возможность появления систематической ошибки при оценке параметра
с некоторым отклонением. Для несмещенных оценок устраняется возможность появления систематической ошибки при оценке параметра 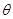 . Статистика
. Статистика 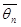 зависит от объема выборки
зависит от объема выборки 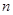 , и при ее удачном построении естественно ожидать, что при больших
, и при ее удачном построении естественно ожидать, что при больших 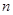 значение статистики приближается к истинному значению параметра
значение статистики приближается к истинному значению параметра 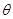 .
.
Если для любого 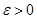
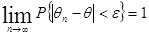 ,
,
то оценка 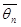 называется состоятельной. Это условие означает, что
называется состоятельной. Это условие означает, что 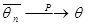 (
(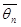 стремится к
стремится к 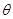 по вероятности), так что при больших
по вероятности), так что при больших 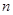 отклонение
отклонение 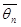 от
от 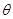 становится сколь угодно малым.
становится сколь угодно малым.
Оценкой качества несмещенной оценки является ее дисперсия. Несмещенная оценка 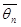 называется эффективной, если ее дисперсия
называется эффективной, если ее дисперсия
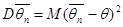
является наименьшей среди дисперсий всех возможных оценок параметра 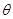 , вычисленных по одному и тому же объему выборки
, вычисленных по одному и тому же объему выборки 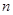 .
.
2. Точечные оценки. Метод моментов.
Оценки 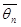 называются точечными, так как они оценивают одно численное значение параметра
называются точечными, так как они оценивают одно численное значение параметра 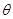 (точку).
(точку).
Рассмотрим повторную выборку 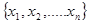 значений генеральной совокупности Х. При этом случайные величины
значений генеральной совокупности Х. При этом случайные величины 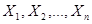 будут независимыми. Пусть
будут независимыми. Пусть 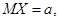
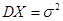 - генеральные средняя и дисперсия совокупности. В качестве оценок для
- генеральные средняя и дисперсия совокупности. В качестве оценок для 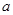 и
и 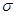 рассмотрим среднюю арифметическую выборки
рассмотрим среднюю арифметическую выборки
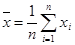
и выборочную дисперсию
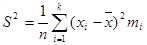 .
.
Оценка 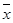 для математического ожидания
для математического ожидания 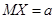 является несмещенной, состоятельной и эффективной. Ее дисперсия равна
является несмещенной, состоятельной и эффективной. Ее дисперсия равна
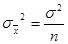 .
.
Оценка 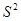 для дисперсии
для дисперсии 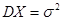 является состоятельной и смещенной. Поэтому на практике часто пользуются несмещенной оценкой
является состоятельной и смещенной. Поэтому на практике часто пользуются несмещенной оценкой
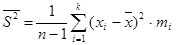
Исправленной выборочной дисперсией называется оценка 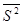 для дисперсии
для дисперсии 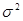 , определяемая формулой
, определяемая формулой 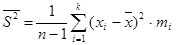 .
.
Для бесповторной выборки оценки 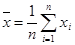 и
и 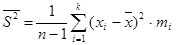 также являются несмещенными и состоятельными, а дисперсия
также являются несмещенными и состоятельными, а дисперсия 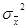 равна
равна 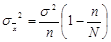 , где N – объем генеральной совокупности. При
, где N – объем генеральной совокупности. При 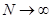 бесповторная выборка не отличима от повторной и формула
бесповторная выборка не отличима от повторной и формула 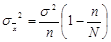 переходит в формулу
переходит в формулу 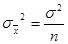 .
.
Путь генеральная совокупность содержит 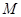 элементов, обладающих некоторым признаком
элементов, обладающих некоторым признаком 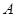 .
.
Генеральной долей признака 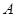 называется величина
называется величина 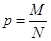 .
.
Для доли 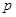 несмещенной и состоятельной оценкой будет выборочная доля
несмещенной и состоятельной оценкой будет выборочная доля 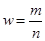 , где
, где 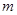 – число элементов выборки, обладающих признаком
– число элементов выборки, обладающих признаком 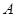 .
.
Дисперсия 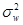 в случае повторной выборки равна
в случае повторной выборки равна 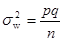 , а случае бесповторной выборки
, а случае бесповторной выборки 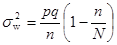 , где
, где 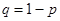 .
.
Если 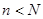 (
(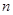 намного меньше
намного меньше 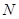 ), то повторная выборка практически не отличается от бесповторной и формулы
), то повторная выборка практически не отличается от бесповторной и формулы 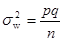 и
и 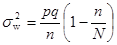 дают одинаковый результат. Если же
дают одинаковый результат. Если же 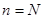 , то объем выборки равен объему генеральной совокупности и выборочная доля равна генеральной, тогда
, то объем выборки равен объему генеральной совокупности и выборочная доля равна генеральной, тогда 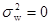 .
.
В случае, когда 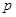 неизвестно, его заменяют выборочным значением
неизвестно, его заменяют выборочным значением 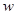 .
.
3. Интервальные оценки параметров .
Точечная оценка 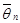 параметра
параметра 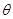 дает лишь некоторое приближенное значение
дает лишь некоторое приближенное значение 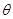 . Чтобы получить представление о точности и надежности оценки, используют интервальную оценку параметра.
. Чтобы получить представление о точности и надежности оценки, используют интервальную оценку параметра.
Интервальной оценкой параметра 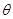 называется интервал
называется интервал 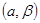 , который с заданной вероятностью
, который с заданной вероятностью 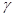 накрывает неизвестное значение параметра
накрывает неизвестное значение параметра 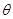 .
.
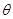
 |
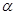
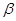
Такой интервал 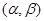 называется доверительным интервалом, а вероятность
называется доверительным интервалом, а вероятность 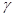 - доверительной вероятностью или уровнем надежности. Обычно доверительный интервал симметричен относительно оценки
- доверительной вероятностью или уровнем надежности. Обычно доверительный интервал симметричен относительно оценки 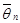 , тогда он определяется формулой
, тогда он определяется формулой
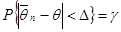
и имеет вид
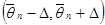 ,
,
т.е. неравенства
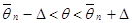
выполняются с вероятностью 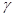 .
.
Наибольшее отклонение 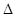 выборочного значения параметра от его истинного значения называется предельной ошибкой выборки.
выборочного значения параметра от его истинного значения называется предельной ошибкой выборки.
4. Доверительная вероятность .
Надежностью (доверительной вероятностью) оценки q по статистической оценке q* называется вероятность 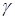 , с которой осуществляется неравенство
, с которой осуществляется неравенство 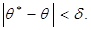 Обычно надежность оценки задается наперед, причем в качестве
Обычно надежность оценки задается наперед, причем в качестве 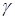 берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
Пусть вероятность того, что 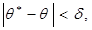 равна
равна 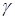 :
:
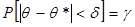 .
.
Заменив неравенство 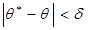 равносильным ему двойным неравенством
равносильным ему двойным неравенством 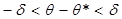 или
или 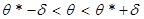 , имеем
, имеем 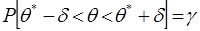 .
.
Это соотношение следует понимать так: вероятность того, что интервал 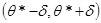 заключает в себе (покрывает) неизвестный параметр
заключает в себе (покрывает) неизвестный параметр 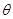 , равна
, равна 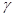 .
.
Доверительным называют интервал 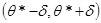 , который покрывает неизвестный параметр с заданной надежностью
, который покрывает неизвестный параметр с заданной надежностью 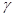 .
.
Пусть 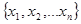 - выборка из генеральной совокупности объема
- выборка из генеральной совокупности объема 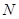 ,
, 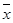 - выборочное среднее,
- выборочное среднее, 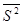 - выборочная дисперсия,
- выборочная дисперсия, 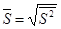 - выборочное среднее квадратическое отклонение,
- выборочное среднее квадратическое отклонение, 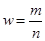 - выборочная доля признака.
- выборочная доля признака.
Доверительный интервал уровня надежности 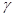 для генеральной средней
для генеральной средней 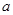 имеет вид
имеет вид
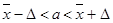 , где
, где 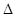 - предельная ошибка выборки, зависящая от
- предельная ошибка выборки, зависящая от 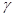 .
.
При 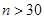 для повторной выборки
для повторной выборки
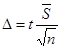 ,
,
а для бесповторной выборки
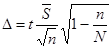 .
.
Здесь 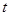 определяется из условия
определяется из условия
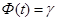 ,
,
где 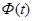 - функция Лапласа.
- функция Лапласа.
Если 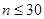 , то доверительный интервал для
, то доверительный интервал для 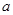 строится только для нормальной генеральной совокупности. Для повторной выборки
строится только для нормальной генеральной совокупности. Для повторной выборки 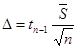 .
.
Здесь 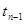 определяется из условия
определяется из условия 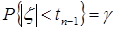 , где случайная величина
, где случайная величина 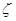 имеет распределение Стьюдента с
имеет распределение Стьюдента с 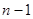 степенями свободы и
степенями свободы и 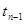 находится по таблицам распределения Стьюдента.
находится по таблицам распределения Стьюдента.
Для бесповторной выборки
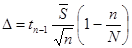 .
.
Доверительный интервал для генеральной доли 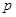 равен
равен 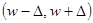 , т.е.
, т.е. 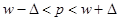 , где при
, где при 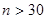 для повторной выборки
для повторной выборки 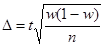 , а для бесповторной выборки
, а для бесповторной выборки 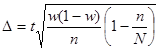 , где
, где 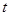 определяется равенством
определяется равенством 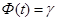 .
.
При 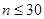 рассматриваются только выборки из нормальной совокупности. Для повторной выборки
рассматриваются только выборки из нормальной совокупности. Для повторной выборки 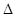 определяется по формуле
определяется по формуле 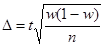 , а для бесповторной – по формуле
, а для бесповторной – по формуле 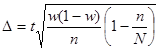 .
.
Пример 1. Из партии в 5000 электрических ламп было отобрано 300 по схеме бесповторной выборки. Средняя продолжительность горения ламп в выборке оказалась равной 1450 часам, а дисперсия – 4000. Найти доверительный интервал для среднего срока горения лампы с надежностью 0,9996.
Для 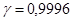 по таблицам находим
по таблицам находим 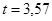 . При
. При 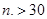 для бесповторной выборки
для бесповторной выборки
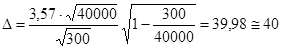
Тогда искомый доверительный интервал
1410 < 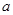 < 1490.
< 1490.
ЛЕКЦИЯ 15. СТАТИСТИЧЕСК АЯ ПРОВЕРКА ГИПОТЕЗ.
Цель: Закрепить понятия статистической, нулевой и конкурирующей гипотез, ошибок первого и второго рода, критической области. Уметь применять критерий Пирсона при решении задач.
Ключевые слова: статистическая, нулевая и конкурирующая гипотезы, ошибки первого и второго рода, критическая область, Критерий Пирсона.
План лекции:
1. Общая схема проверки.
2. Сравнение двух дисперсий нормальных генеральных совокупностей.
3. Критерии проверки гипотез. Критерий Пирсона.
1. Общая схема проверки
Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений.
Например, статистическими являются гипотезы:
1) генеральная совокупность распределена по закону Пуассона;
2) дисперсии двух нормальных совокупностей равны между собой.
В первом гипотезе сделано предложение о виде неизвестного распределения, во второй – о параметрах двух известных распределений.
Гипотеза «на Марсе есть жизнь» не является статистической, поскольку в ней не идет речь ни о виде, ни о параметрах распределения.
Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать.
Нулевой (основной) называют выдвинутую гипотезу Но.
Конкурирующей (альтернативной) называют гипотезу Н1, которая противоречит нулевой.
Например, если нулевая гипотеза состоит в предположении, что математическое ожидание а нормального распределения равно 10, то конкурирующая гипотеза, в частности, может состоять в предположении, что 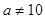 . Коротко это записывают так:
. Коротко это записывают так: 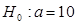 ;
; 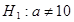 .
.
Различают гипотезы, которые содержат только одно и более одного предположений.
Простой называют гипотезу, содержащую только одно предположение. Например, если 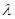 - параметр показательного распределения, то гипотеза
- параметр показательного распределения, то гипотеза 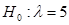 - простая. Гипотеза
- простая. Гипотеза 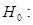 математическое ожидание нормального распределения равно 3 (
математическое ожидание нормального распределения равно 3 (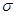 известно) – простая.
известно) – простая.
Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. Например, сложная гипотеза 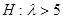 состоит из бесчисленного множества простых вида
состоит из бесчисленного множества простых вида 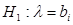 , где
, где 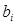 - любое число, большее 5. Гипотеза
- любое число, большее 5. Гипотеза 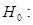 математическое ожидание нормального распределения равно 3
математическое ожидание нормального распределения равно 3 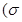 неизвестно) – сложная.
неизвестно) – сложная.
Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки двух родов.
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Подчеркнем, что последствия этих ошибок могут оказаться весьма различными. Например, если отвергнуто правильное решение «продолжать строительство жилого дома», то эта ошибка первого рода повлечет материальный ущерб; если же принято неправильное решение «продолжать строительство», несмотря на опасность обвала стройки, то эта ошибка второго рода может повлечь гибель людей. Можно привести примеры, когда ошибка первого рода влечет более тяжелые последствия, чем ошибка второго рода.
Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.
Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.
Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают.
Поскольку критерий К – одномерная случайная величина, все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами и, следовательно, существуют точки, которые их разделяют.
Критическими точками (границами) 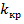 называют точки, отделяющие критическую область от области принятия гипотезы.
называют точки, отделяющие критическую область от области принятия гипотезы.
Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.
Правосторонней называют критическую область, определяемую неравенством 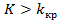 , где
, где 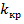 - положительное число.
- положительное число.
Левосторонней называют критическую область, определяемую неравенством 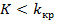 , где
, где 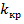 - отрицательное число.
- отрицательное число.
Односторонней называют правостороннюю или левостороннюю критическую область.
Двусторонней называют критическую область, определяемую неравенствами 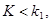
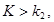 где
где 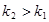 .
.
В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствами (в предположении, что 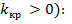
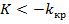
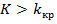
или равносильным неравенством 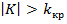 .
.
 2015-02-27
2015-02-27 15775
15775
