Передаточные функции

Рассмотрим элемент системы автоматического управления (рис. 2.1), выходная величина которого y является функцией двух переменных: управляющего воздействия x и возмущающего f. Математически это запишется как

.

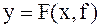(2.1)

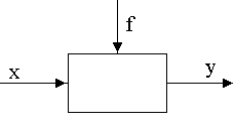
Рисунок 2.1 – Элемент системы автоматического управления

Линейное дифференциальное уравнение элемента в общем случае имеет вид:

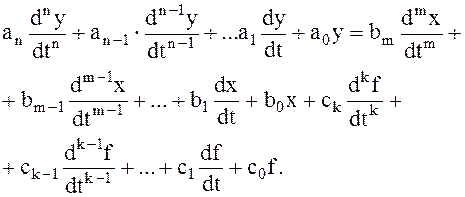
(2.2)

Подобное уравнение (особенно высокого порядка) удобнее всего решать операторным методом.

Известно, что изображение функции x(t) имеет вид [12]:

.

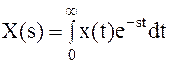(2.3)

Операция перехода от изображения к оригиналу называется обратным преобразованием Лапласа

.

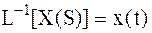(2.4)

Изображения различных функций представлены в таблице 2.1. Эта же таблица позволяет найти функцию по ее изображению, то есть произвести обратное преобразование Лапласа.

Найдем изображение производной .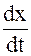

Пусть

.

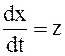(2.5)

В соответствии с выражением (2.3)

.

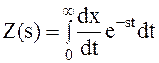(2.6)

Пусть ,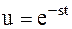

,

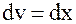(2.7)

т.е. .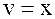

Известно, что [12]

,

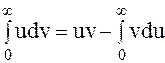(2.8)

тогда:

.

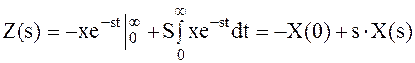(2.9)