Пусть на вход нелинейного звена подается гармонический сигнал:
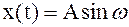 t. t.
| (2.207) |
Тогда на его выходе появится сигнал:
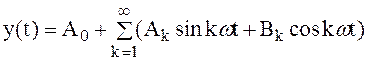 , ,
| (2.208) |
то есть сигнал, равный сумме гармонических сигналов высших гармоник. Сделаем предположение, что всеми гармониками, кроме первой, можно пренебречь, то есть 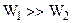 .
.
Тогда
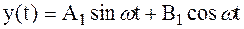 , ,
| (2.209) |
Из (2.207) следует, что
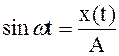 , ,
| (2.210) |
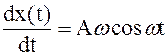 , ,
| (2.211) |
Отсюда
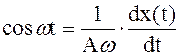
| (2.212) |
и
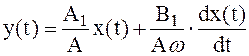 . .
| (2.213) |
Переходя к изображению, получим:
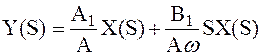 . .
| (2.214) |
Отсюда передаточная функция:
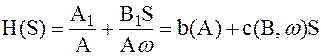 . .
| (2.215) |
В выражении (2.215) b и c зависят от вида нелинейности. Их можно задать в виде таблицы. При отсутствии гистерезиса с = 0.
Таким образом, нелинейные системы можно рассчитывать как линейные, выбрав один из способов линеаризации.
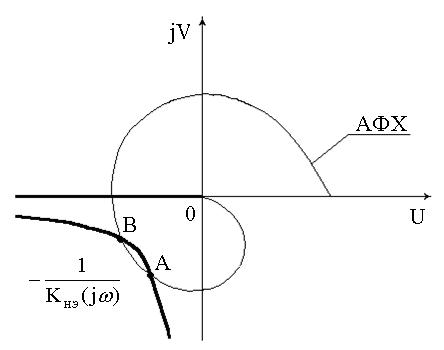
Рисунок 2.83 – Графический способ расчета
нелинейной системы
Расчет нелинейной системы методом гармонической линеаризации производится в следующем порядке:
1. Строится АФХ линейной части (рис. 2.83).
2. Строится обратная комплексная передаточная функция нелинейной части 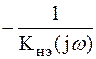 , где
, где
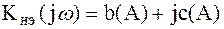 . .
| (2.216) |
При отсутствии гистерезиса эта функция проходит по оси абсцисс, при наличии гистерезиса она пересекает АФХ в двух точках. Точка выхода из контура является точкой устойчивого равновесия, а точка входа в контур точкой неустойчивого равновесия.
 2015-02-27
2015-02-27 350
350








