Основные формулы. 1.Поступательное движение

1.Поступательное движение

1. Кинематическое уравнение движения материальной точки (центра масс тела) вдоль оси х: x=f(t),

где f(t) –некоторая функция от времени.

2. Средняя скорость: < V_x >=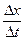

3. Средняя путевая скорость: < V >=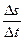

где D s - путь, пройденный точкой за интервал D t. Путь D s в отличии от разности координат (D х=х₂-х₁) не может убывать и принимать отрицательные значения, т.е. D s ³0. Поэтому < V > ³ |< V_x >|.

4. Мгновенная скорость: V_x = .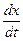

5. Среднее ускорение: < а_x >=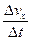

6. Мгновенное ускорение: а_x = .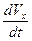

2. Вращательное движение.

7.Кинематическое уравнение движения материальной точки по окружности: j=f(t); r=R=const.

8.Угловая скорость: w=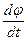

9.Угловое ускорение: e=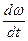

10.Связь между линейными и угловыми величинами, характеризующими движение точки по окружности:

v=w×R; a_t=e×R; a_n=w²×R,

где v – линейная скорость, a_t и a_n - тангенциальное и нормальное ускорения; w - угловая скорость; e - угловое ускорение; R -радиус окружности.

11.Полное ускорение: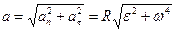

12.Угол между полным ускорением 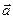и нормальным 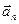: a=arccos()

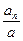3.Колебательное движение и волны.

13.Кинематическое уравнение гармонических колебаний материальной точки: x=A×cos(wt+j),

где х- смещение; А - амплитуда колебаний; w - круговая или циклическая частота; j - начальная фаза.

14.Скорость материальной точки, совершающей гармонические колебания: v=-A×w×sin(wt+j),

15.Ускорение материальной точки, совершающей гармонические колебания: a=-A×w²×cos(wt+j),

16.Сложение гармонических колебаний одного направления и одинаковой частоты:

а) амплитуда результирующего колебания: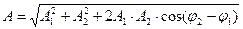

б) начальная фаза результирующего колебания: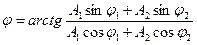

17.Траектория точки, учавствующей в двух взаимно- перпендикулярных колебаниях: (x=A₁×coswt, y=A₂×cos(wt+j)):

a) 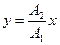(если разность фаз j =0);

b) 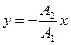(если разность фаз j =± p);

c) 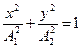(если разность фаз j =± );

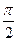18.Уравнение плоской бегущей волны: у=A×cosw(t- ),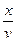

где у - смещение любой из точек среды с координатой х в момент t; v - скорость распространения колебаний в среде.

19.Связь разности фаз D j колебаний с расстоянием D х между точками среды, отсчитанным в направлении распространения колебаний: D j= 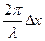, где l - длина волны.