1. Закон Кулона: 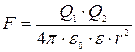
где F –сила взаимодействия точечных зарядов Q 1 и Q 2, r -расстояние между зарядами; e -диэлектрическая проницаемость; e 0=8,85×10-12 Ф/м –электрическая постоянная.
2. Напряженность электрического поля и потенциал: 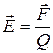 и
и 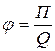
где П — потенциальная энергия точечного положительного заряда Q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).
3. Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда: 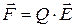 и П=Q×j
и П=Q×j
4. Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей): 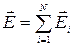 и
и 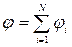 ,где E i, (j i — напряженность и потенциал в данной точке поля, создаваемого i -м зарядом).
,где E i, (j i — напряженность и потенциал в данной точке поля, создаваемого i -м зарядом).
5. Напряженность и потенциал поля, создаваемого точечным зарядом:
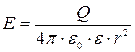 и
и 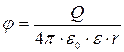 , где r — расстояние от заряда Q до точки, в которой определяются напряженность и потенциал.
, где r — расстояние от заряда Q до точки, в которой определяются напряженность и потенциал.
6. Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиуса R на расстоянии r от центра сферы:
а) если r < R, то Е = 0; 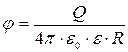
б) ecли r = R, то 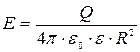 ;
; 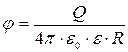
в) ecли r > R, то 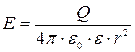 ;
; 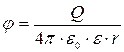
где Q –заряд сферы.
7. Линейная плотность заряда (заряд, приходящийся на единицу длины заряженного тела): t=Q/l
8. Поверхностная плотность заряда (заряд, приходящийся на единицу площади поверхности заряженного тела): s=Q/S
9. Напряженность и потенциал поля, создаваемого распределенными зарядами. Если заряд равномерно распределен вдоль линии с линейной плотностью t, то на линии выделяется малый участок длины dl с зарядом dQ = t×dl. Такой заряд можно рассматривать как точечный. Напряженность dE и потенциал dj электрического поля, создаваемого зарядом dQ, определяется формулами: 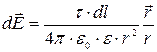 и
и 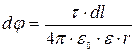
где ` r — радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.
Используя принцип суперпозиции электрических полей, находим интегрированием напряженность Е и потенциал j поля, создаваемого распределенным зарядом.
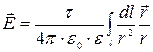 и
и 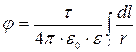
Интегрирование ведется вдоль всей длины заряженной лини.
10. Напряженность поля, создаваемого бесконечной прямой равномерно заряженной линией или бесконечно длинным цилиндром: 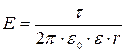
где r — расстояние от нити или оси цилиндра до точки, напряженность поля в которой вычисляется.
11. Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью: 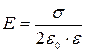
12. Напряженность поля между двумя равномерно и разноименно заряженными бесконечными параллельными плоскостями: 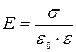
13. Связь потенциала с напряженностью:
а) в общем случае: ` Е = -grad j, или 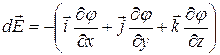
б) в случае однородного поля: 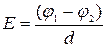
в) в случае поля, обладающего центральной или осевой симметрией: 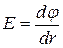
14. Сила притяжения между двумя разноименными заряженными обкладками конденсатора: 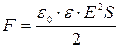
15. Электрический момент диполя: `p=|Q|×`l
где Q — заряд; `l - плечо диполя (величина векторная, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
16. Работа сил поля по перемещению заряда Q из точки поля с потенциалом j 1 в точку с потенциалом j 2: А 12= Q× (j 1 - j 2)
17. Электроемкость: С = Q / j или С = Q / U,
где j -потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U –разность потенциалов пластин конденсатора.
18. Электроемкость уединенной проводящей сферы радиуса R: C= 4× p×e×e 0 ×R
19. Электроемкость плоского конденсатора: 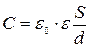 , где S –площадь пластины (одной) конденсатора; d – расстояние между пластинами.
, где S –площадь пластины (одной) конденсатора; d – расстояние между пластинами.
20. Электроемкость слоистого конденсатора: 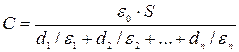 , где S –площадь пластины (одной) конденсатора; d – расстояние между пластинами.
, где S –площадь пластины (одной) конденсатора; d – расстояние между пластинами.
21. Электроемкость батареи конденсаторов:
а) при последовательном соединении: 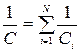 ;
;
а) при параллельном соединении: 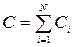 ;
;
где N - число конденсаторов в батарее.
22. Энергия заряженного конденсатора: 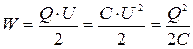 .
.
23. Сила тока: I=Q / t, где Q –заряд, прошедший через поперечное сечение проводника за время t.
24. Плотность тока: j = I / S, где S –площадь поперечного сечения проводника.
25. Связь плотности тока со средней скоростью < V >- направленного движения заряженных частиц: j=e×n×<V>,
где е — заряд частицы; п — концентрация заряженных частиц.
26. Закон Ома:
а) для участка цепи, не содержащего э. д. с.: 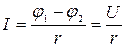
где j 1 - j 2 = U -разность потенциалов (напряжение) на концах участка цепи; r -сопротивление участка;
б) для участка цепи, содержащего э. д. с.: 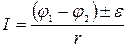
где e -э.д.с. источника тока; r –полное сопротивление участка (сумма внешних и внутренних сопротивлений);
в) для замкнутой (полной) цепи: 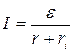
где r –внешнее сопротивление цепи; r 1 –внутреннее сопротивление цепи.
27. Законы Кирхгофа:
а) первый закон: 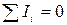 ,
,
где 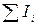 — алгебраическая сумма сил токов, сходящихся в узле;
— алгебраическая сумма сил токов, сходящихся в узле;
б) второй закон: 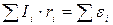
где 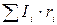 -алгебраическая сумма произведений сил токов на сопротивления участков;
-алгебраическая сумма произведений сил токов на сопротивления участков; 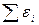 -алгебраическая сумма э.д.с.
-алгебраическая сумма э.д.с.
28. Сопротивление r и проводимость G проводника: 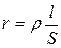 ;
; 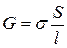
где r -удельное сопротивление; j – удельная проводимость; l -длина проводника; S - площадь поперечного сечения проводника.
29. Зависимость удельного сопротивления от температуры: rt=r0 × (1+ a×t)
30. Сопротивление системы проводников:
а) при последовательном соединении: 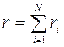
б) при параллельном соединении: 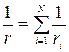
где r i -сопротивление i -го проводника.
31. Работа тока: A=I×U×t=I 2× r×t= 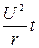
Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение U, последние две – для участка, не содержащего э.д.с.
32. Мощность тока: Р=I×U=I 2× r = 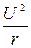
33 Закон Джоуля -Ленца: Q= I 2× r×t
34. Закон Ома в дифференциальной форме: j=s×`E
где s - удельная проводимость, ` E -напряженность электрического поля, j –плотность тока.
35. Связь удельной проводимости с подвижностью b заряженных частиц (ионов): s=Q×n× (b+ + b-),
где Q -заряд иона; п -концентрация ионов; b+ и b- - подвижности положительных и отрицательных ионов.
36. Коэффициент полезного действия источника тока: 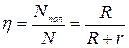
 2015-02-27
2015-02-27 486
486








