Задача №1

Задание: Для заданного чугунного стержня (рис.1) из условия прочности подобрать площадь поперечного сечения. Построить эпюру перемещений сечений стержня.

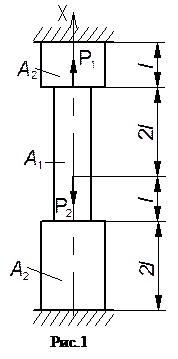Исходные данные:

l = 150 мм; P₁ = 3Р; P₂ = Р; Р = 100кН; площади поперечных сечений участков - А₁= 2F, А₂= 3F. Материал стержня чугун СЧ21-40, Е=120000 МПа, s_вр = 210 МПа, s_вс = 1000 МПа. Коэффициент запаса прочности для чугуна n = 2.

Решение:

1).Определим допускаемые напряжения для материала стержней:

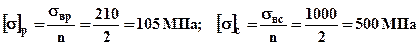
2). Рассмотрим равновесие стержня, отбросив заделки и заменив их неизвестными реакциями R₁, R₂ (см. рис.2) для их определения имеется 1 уравнения равновесия 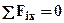из которого следует 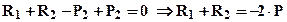. Таким образом, система один раз статически неопределима.

3). Далее, для раскрытия статической неопределимости следует составить уравнение совместности деформаций, в рассматриваемом примере таким уравнением может быть: 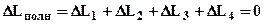- (1) - отражающее тот факт, что из-за наличия жестких опор длина стержня не изменяется. Удлинения участков стержня можно выразить по закону Гука через нормальные силы в сечениях:

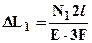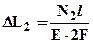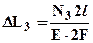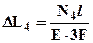; ; ; , нумерация участков принята снизу вверх. Нормальные силы выразим через неизвестные реакции и внешнюю нагрузку методом сечений: проводя произвольное поперечное сечение в пределах каждого из участков, отбрасываем любую часть и заменяем ее реакцией взаимодействия частей, которая и является нормальной силой (см. рис.2). Примечание: неизвестные нормальные силы в сечениях следует показывать всегда в положительном направлении, то есть так, чтобы они были растягивающими. Из условий равновесия рассматриваемых частей находим нормальные силы: 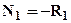; ; 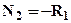; 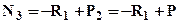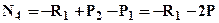(2).

Подставляя выражения для нормальных сил в выражения для удлинений участков, а затем в уравнение совместности деформаций получим следующее уравнение: 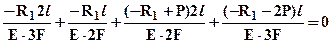- (2), разрешая которое относительно R₁ найдем - 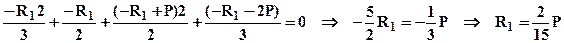. Таким образом, статическая неопределенность раскрыта.

Теперь можно рассчитать нормальные силы:

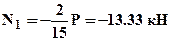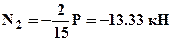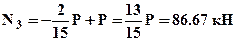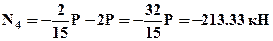; ; ; , и выразить нормальные напряжения в сечениях: 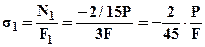; ; 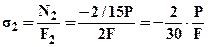; 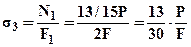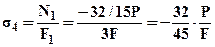- (3). Теперь необходимо записать два условия прочности:

а). По максимальным сжимающим напряжениям 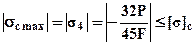откуда требуемая площадь определится как 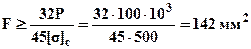; б). По максимальным растягивающим напряжениям 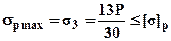откуда требуемая площадь определится как 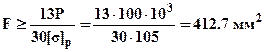. Так как должны выполнятся одновременно оба условия прочности то следует принять площадь 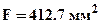. Тогда напряжения 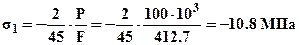; ; 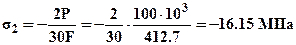; 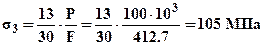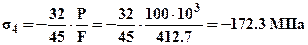. По рассчитанным значениям построим эпюры N и s (см. рис3).

Вычисляем удлинения участков стержней: 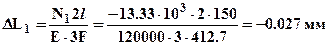; ; 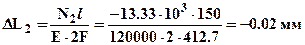; 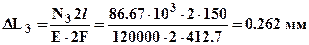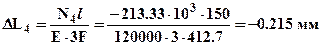. Убедимся что, условие совместности деформаций выполняется - 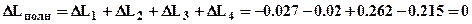. Строим эпюру d - смещений поперечных сечений стержня. Примем за отсчетное сечение нижнюю заделку стержня, а за положительное направление смещение сечений вверх, тогда если участок стержня растягивается, то его сечения перемещаются в положительном направлении. Легко доказать, что при N = const эпюра смещений в пределах участка будет линейной, следовательно, для построения эпюры смещений достаточно вычислить перемещения сечений находящихся на границах участков. Смещение верхней границы 1-го участка - 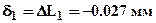, 2-го - 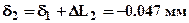, 3-го - .

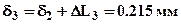По рассчитанным значениям строим эпюру d (см. рис.3), учитывая, что на границах участков разрыва эпюры быть не может и в заделках перемещение равно нулю.

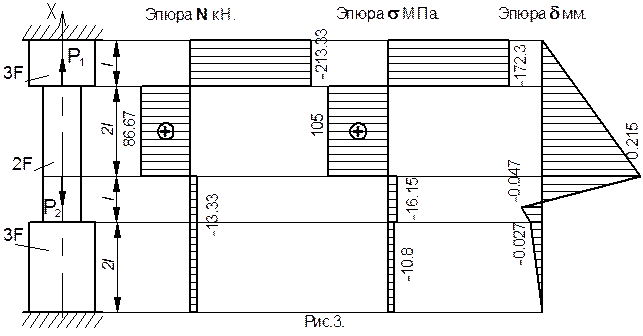
Более сложная постановка задачи. (с учетом температурных и монтажных напряжений).

Будем считать, что температура стержня после сборки была повышена на DТ = 200°. В свободном (незакрепленном) состоянии удлинился бы на величину - D_Т = a×DТ×L_п, где a=1.1×10^-5 град^-1- коэффициент линейного расширения материала стержня (СЧ21-40), L_п=6l – полная длина стержня: 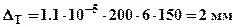. Закрепления стержня не позволяют ему удлинится и при повышении температуры стержень окажется сжатым на величину D_Т (при понижении температуры соответственно растянутым). Тогда уравнение совместности деформаций (1) перепишется в виде 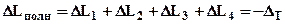(1¢). Используя принцип суперпозиции нагрузок, найдем отдельно напряжения возникающие при изменении температуры и затем сложим их с напряжениями от внешней нагрузки, которые были найдены ранее. При отсутствии внешних нагрузок уравнение (2) предстанет в ви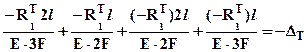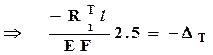де: где 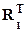реакция возникающая только от изменения температуры. Решая это уравнение, найдем 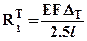, при этом нормальные силы: 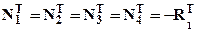тогда нормальные напряжения, возникающие только от изменения температуры 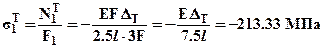, , 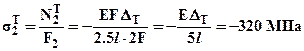, 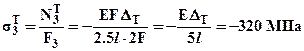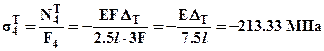. Заметим, что эти напряжения не зависят от величины площади поперечных сечений и условие прочности выполняется 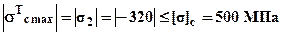, (если это условие не выполняется то прочность стержня за счет подбора площади сечений обеспечить невозможно, необходимо уменьшать температурные напряжения). Складывая температурные напряжения с напряжениями от внешней нагрузки (3) получим следующие выражения:

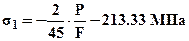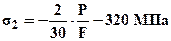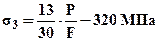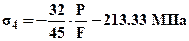; ; ; - (3¢).

Теперь снова определим площадь поперечных сечений из условий прочности. Анализ выражений (3¢) показывает, что теоретически растянутым может оказаться только участок №3, записывая для него условие прочности 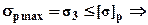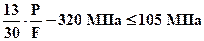определим площадь 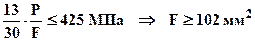. Максимальное сжимающее напряжение будет действовать в участке №2 или №4. Записывая условия прочности участка №2 найдем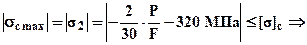 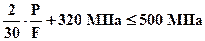площадь 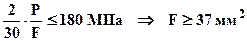. Из условия прочности для участка №4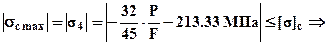 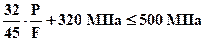площадь 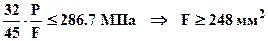. Для удовлетворения одновременно всем условиям прочности мы должны принять площадь 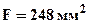. Интересно отметить, что при одновременном действии внешних нагрузок и температуры площадь поперечного сечения необходимая для обеспечения прочности оказывается существенно меньше, чем в первом варианте. Это объясняется тем, что при действии только внешних сил опасным является растянутый 3-й участок, при повышении температуры все участки испытывают дополнительное сжатие и опасным становится сжатый участок №4 чугун же имеет большую прочность на сжатие чем на растяжение. Окончательно принять площадь 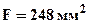можно только в случае если внешняя нагрузка и температура изменяются синхронно. Если же нагрузки могут прикладыватся по отдельности, то опасным состоянием в рассматриваемом примере будет действие только внешних сил и следует принять .

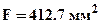Примечание. Точно так же решается задача в случае монтажных напряжений, когда стержень имеет начальную длину, отличающуюся от номинальной (равной расстоянию между опорами) на величину D. Во всех вышеприведенных расчетах нужно D_Т заменить на D. Величина D - считается положительной, если начальная длина стержня больше номинальной.

ЗАДАЧА №2

Задание: Для стержневой конструкции (рис.1) из условия прочности подобрать максимально допускаемую внешнюю нагрузку (выраженную через q).

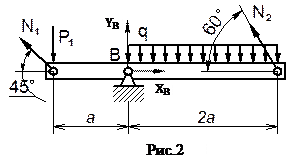
Исходные данные: F = 300 мм²; l = 600 мм; a = 1000 мм; P₁ = 3 qa; Материал стержней чугун СЧ32-52, Е=1.1×10⁵ МПа, s_вр = 320 МПа, s_вс = 1200 МПа. Определим допускаемые напряжения для материала стержней:

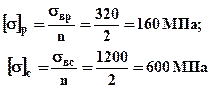
Решение: Рассмотрим равновесие абсолютно жесткого бруса, отбросив стержни (рис.2). В данном случае рациональнее заменить отброшенные стержни нормальными силами N₁, N₂, N₃, возникающими в них (примечание: неизвестные нормальные силы в стержнях следует показывать всегда в положительном направлении, то есть так, чтобы они были растягивающими). Имеется 3 уравнения равновесия и 4 неизвестных: N₁, N₂, Y_B, X_B, следовательно, система один раз статически неопределима. Из трех уравнений равновесия имеет смысл составить только одно, содержащее нужные неизвестные N₁, N₂, в данном случае это: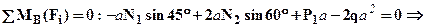

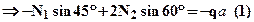. Необходимо составить одно уравнение совместности деформаций. Для этого рассмотрим возможное деформированное состояние конструкции В данном случае таким состоянием будет поворот жесткого бруса вокруг шарнира В, показанное на рис.3 (совершенно необязательно, чтобы выбранное направление перемещения и поворота совпадало с действительным). Шарниры А, С займут новые положения А₁, С₁, их вертикальные перемещения обозначим соответственно y_а, y_с. (В силу малости перемещений и деформаций можно заменить дуги окружностей, по которым перемещаются шарниры, вертикальными отрезками АА₁ и СС₁. Кроме того, можно считать, что углы наклона стержней не изменились). Очевидно, что перемещения y_а, y_с связаны между собой условием, 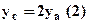, которое получается из подобия треугольников АВА₁ и ВСС₁. Очевидно, что эти перемещения связаны с абсолютными удлиннениями стержней следующими зависимостями: 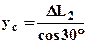, 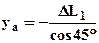(3), знак «-» учитывает, что первый стержень сжат. Эти зависимости получены из рассмотрения рис.4.

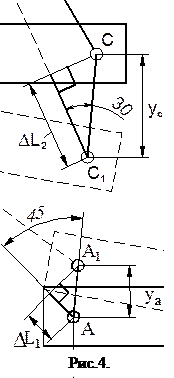Следовательно: 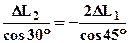и выражая ΔL по закону Гука, получим: . Учитывая, что F₁ = F, F₂ = 2F, l₁ = l/sin45°, l₂ = 2l/sin60° получим:

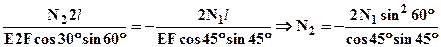
или подставляя значения 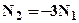(4). Подставляя (4) в выражение (1) выразим нормальные силы в стержнях:

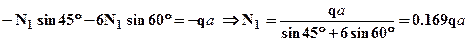
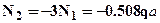. Нормальные напряжения в стержнях выразятся следующим образом:

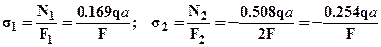(5). Из условий прочности определим допускаемую внешнюю нагрузку. Для первого стержня, 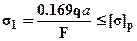следовательно:

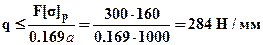. Для второго стержня: 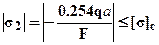(здесь учтено, что при составлении условия прочности по сжимающим напряжениям расчетные напряжения всегда берутся по модулю, так как допускаемые напряжения всегда положительны), следовательно: 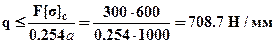. Из двух нагрузок выбираем меньшую, так как должны выполнятся условия прочности для обоих стержней, таким образом, окончательно принимаем максимально допускаемую внешнюю нагрузку 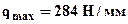.Для проверки вычислим напряжения в стержнях: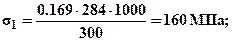 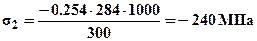- условие прочности выполнено для обоих стержней.

Более сложная постановка задачи. (с учетом монтажных напряжений)

Будем считать, что стержень №1 до сборки конструкции имел длину отличающуюся от номинальной на малую величину D = - 0.6 мм (знак “-” означает, что начальная длина меньше номинальной). Используя принцип суперпозиции нагрузок, найдем отдельно монтажные напряжения и затем сложим их с напряжениями возникающими от внешней нагрузки. При отсутствии нагрузок уравнение равновесия (1) предстанет в виде:

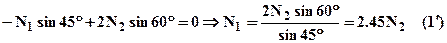. Уравнение (3) для 2^-го стержня не изменится, а для 1^-го запишется в виде: 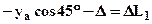, см. рис.5 (на рис.5 формально показана ситуация соответствующая положительному D). Уравнение совместности деформаций тогда запишется в виде:

.

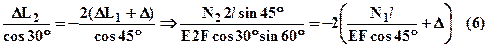Подставляя (1¢) в последнее выражение после элементарных преобразований получим: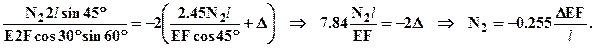

Подставляя значения, вычислим нормальные силы и монтажные напряжения в стержнях:

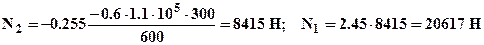
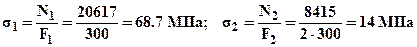. Оба стержня после монтажа растянуты (здесь важно отметить, что условия прочности выполнены для обоих стержней, то есть при монтаже их прочность не нарушена). Добавляя монтажные напряжения к напряжениям, возникающим от внешних нагрузок (5) получим выражения для суммарных напряжений в стержнях нагруженной конструкции: 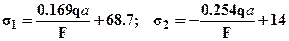. Для определения допускаемой внешней нагрузки можно записать условия прочности для обоих стержней. Очевидно, что первый стержень растянут и из условия прочности для него:

.

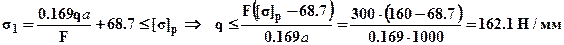Со вторым стержнем дело обстоит сложнее, он может оказаться как сжатым, так и растянутым в зависимости от величины параметра внешней нагрузки – q, и в принципе для второго стержня можно записать условия прочности, как на сжатие так и на растяжение. Однако, если второй стержень растянут (второе слагаемое по модулю больше первого), то наибольшее растягивающее напряжение не превосходит 14МПа (= 14МПа только при отсутствии внешней нагрузки) и меньше допускаемого напряжения на растяжение. Следовательно, для второго стержня имеет смысл записать только условие прочности на сжатие: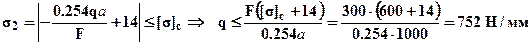

(при подстановке в условие прочности берется модуль напряжения s₂ следовательно меняются на противоположные, знаки у обоих слагаемых в его выражении). Из двух полученных нагрузок выбираем меньшую, таким образом, окончательно принимаем максимально допускаемую внешнюю нагрузку .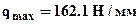

Для проверки вычислим напряжения в обоих стержнях:

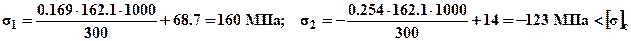
Условия прочности выполняются для обоих стержней, следовательно, самый опасный стержень был выбран правильно. Удлиннения стержней можно определить по формулам:

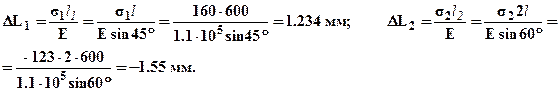
Перемещения: 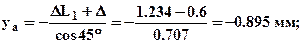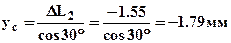удовлетворяют условию совместности перемещений (2). (З нак «-» означает, что действительные перемещения шарниров противоположны показанным на рис.2).