Определение перемещений при поперечном изгибе интегрированием дифференциального уравнения изогнутой оси стержня

(с постоянным по длине сечением)

Деформация стержня при поперечном изгибе представляется в виде прогибов y (перемещений перпендикулярных недеформированной оси) и j поворотов поперечных сечений стержня. Считается, что поперечное сечение стержня после изгиба остается плоским и перпендикулярным изогнутой оси стержня, откуда следует, что 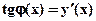. Принято следующее правило знаков: прогиб считается положительным, если направлен вверх; угол поворота считается положительным, если сечение поворачивается против часовой стрелки. Для всех последующих выкладок принята следующая система координат: ось стержня X (в недеформированном состоянии) направлена вправо, ось Y вверх.

Для жестких балок максимальные прогибы, которых малы по сравнению с длиной, следовательно, 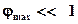связь углов поворота с прогибами упрощается 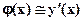. Для определения перемещения в таких балках используется линеаризованное дифференциальное уравнени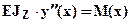е: , где 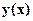- уравнение изогнутой оси стержня (кривая изгиба). В этом дифференциальном уравнении не учитываются перемещениями, связанными с деформацией сдвига (то есть с действием перерезывающей силы) в связи с их малости по сравнению с деформацией связанной с изгибом. Последовательно интегрируя это уравнение два раза, получим соответственно уравнение углов поворота 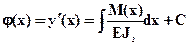уравнение прогибов 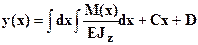. Константы интегрирования 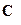и 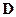определяются из граничных условий.

Непосредственное интегрирование дифференциального уравнения и особенно определение констант интегрирования для балок более чем 2-мя участками является трудоемкой задачей. Так, например, для балки с N участками необходимо записать и проинтегрировать N дифференциальных уравнений при этом появится 2×N констант интегрирования 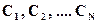; 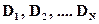и для их определения необходимо записать и использовать 2×N граничных условий. Два граничных условия отражают условия закрепления стержня в опорах. Для каждой шарнирной опоры можно записать 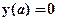, 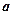- координата сечения, где расположена опора. 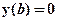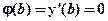Для жесткой заделки и , где 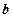- координата жесткой заделки. Остальные 2×N-2 констант интегрирования находятся из условий непрерывного (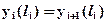) и плавного (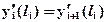) сопряжения изогнутой оси стержня на N-1 границах между участками, здесь 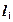- координата границы между i и i +1 участком.

Метод начальных параметров является более удобным для балок со сложной нагрузкой (с большим количеством участков). Суть метода начальных параметров заключается в выравнивания констант интегрирования по участкам, в результате, которого неизвестными остаются лишь две из них 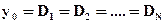, 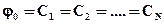. Оставшиеся константы интегрирования имеют простой физический смысл: 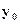- прогиб начального (при x = 0) сечения, 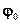- угол поворота начального сечения и определяются из условий закрепления балки. Для произвольной балки постоянного по длине сечения нагруженной k - моментами 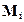и m -сосредоточенными силами 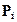(включая реакции опор), а также n - равномерно распределенными нагрузками 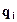уравнения углов поворота и прогибов записываются одним выражением сразу для всей балки (для всех участков):

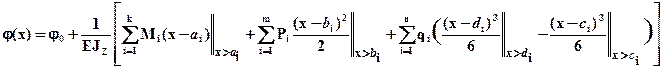
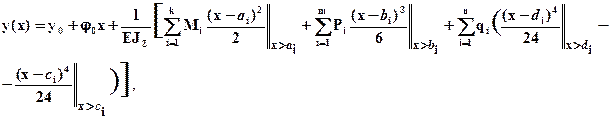
где a _i, b _i - координаты сечений где приложена соответственно i - сосредоточенная сила и i - сосредоточенный момент, c _i, d _i координаты соответственно начала и конца i - равномерной распределенной нагрузки. Двойные черточки у каждого из слагаемых показывают, при каком условии данное слагаемое включается в вычисления, а именно при определении прогибов или углов поворота в произвольном сечении с координатой - x в вышеприведенных выражениях удерживаются только те слагаемые, которые учитывают нагрузки, приложенные к балке левее рассматриваемого сечения. В выражениях метода начальных параметров принято следующее правило знаков для внешних нагрузок: 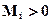если он направлен по часовой стрелке; 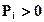и 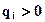если они направлены вверх.

Определение перемещений при поперечном изгибе энергетическими методами.

Рассмотренное выше дифференциальное уравнение неприменимо для стержней с криволинейной осью и для рам. Более универсальными в этом смысле являются энергетические методы. Наиболее популярным является метод Мора (интеграл Мора).

Согласно методу Мора рассматриваются два состояния системы (балки, рамы): грузовое и единичное. Грузовое состояние обусловлено действием на систему заданной внешней нагрузки, возникающие при этом силовые факторы и их эпюры называются грузовыми. Единичное состояние обусловлено действием на систему единичной обобщенной нагрузки приложенной по направлению искомого перемещения, возникающие при этом силовые факторы и их эпюры, называются единичными. Под обобщенной нагрузкой понимается либо сосредоточенная сила, либо сосредоточенный момент. Обобщенной нагрузке соответствуют обобщенные перемещения: сосредоточенной силе соответствует линейное перемещение; моменту соответствует угол поворота сечения.

Пренебрегая перемещениями, связанными с деформацией сдвига ввиду их малости по сравнению с деформацией изгиба интеграл Мора для случая прямого плоского изгиба запишется в виде: , здесь 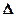- обобщенное перемещение соответствующее приложенной единичной обобщенной нагрузке, 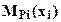выражение грузового изгибающего момента на i - том участке 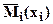выражениеединичного изгибающего момента на i - том участке.

Во всех энергетических методах знак результата означает: знак «+», что искомое перемещение совпадает по направлению с приложенной единичной нагрузкой; знак «-», что искомое перемещение противоположно по направлению приложенной единичной нагрузке.

В инженерной практике широко используется графический способ вычисления интеграла Мора - способ Верещагина. Формула Верещагина в ви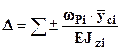де: , где 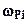- площадь i - го участка грузовой эпюры, 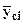ордината эпюры единичного момента взятая под центром тяжести участка грузовой эпюры. Знак «+» перед слагаемым в формуле ставится в случае когда и единичная и грузовая эпюры моментов построены на одноименных волокнах, знак «-» в противном случае. Минимальное количество слагаемых в формуле Верещагина равно количеству участков эпюры единичного момента. Если границы эпюры грузового момента не совпадают с границами эпюры единичного момента, то грузовую эпюру необходимо дополнительно разбить по границе единичной эпюры.

Если имеются трудности с определением площадей и положений центров тяжести участков грузовых эпюр, то для вычисления интеграла Мора рационально использовать формулу Симпсона-Корнаухова: 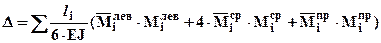, где 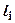- длина i - го участка, 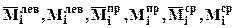- значения единичных и грузовых моментов на левой и правой границе и посередине i – го участка соответственно. Формула Симпсона-Корнаухова справедлива только для стержней с прямолинейными участками (для балок и рам) и только если грузовая эпюра либо линейна, либо является параболой не выше 2-ой степени.

Отметим, что перемещения, определенные с помощью дифференциального уравнения изогнутой оси и с помощью энергетического метода получаются одинаковыми по абсолютной величине.