Задача №2

Задание: Для заданной балки нагруженной в плоскости XY (рис.1) из условия прочности подобрать размеры поперечного сечения в виде нестандартного тавра (сечение показано там же). Определить перемещения и углы поворота некоторых сечений балки, используя дифференциальное уравнение упругой линии балки. Определить перемещения и углы поворота некоторых сечений балки, используя энергетический метод.

Исходные данные: l = 2000 мм; P = 20 кН; М = 10 кНм; q₁ = 15 кН/м; q₂ = 10 кН/м. Материал стержней чугун СЧ15-32, с модулем продольной упругости (модулем Юнга) - Е=1.1×10⁵ МПа и пределами прочности на растяжение и сжатие s_вр = 150 МПа, s_вс = 650 МПа.

Решение:

1).Определим допускаемые напряжения для материала стержней на растяжение и сжатие, коэффициент запаса прочности, учитывая что материал балки хрупкий, примем: n=2:

; .

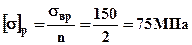2).Определим реакции опор из условий равновесия всей балки (см. рис.1): из суммы моментов относительно первой (левой) опоры получим –

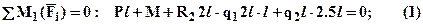
из суммы моментов относительно второй (правой) опоры получим –

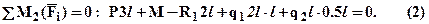
Из уравнения (1) выразим и определим реакцию левой шарнирной опоры R₂ а из уравнения (2) реакцию левой шарнирной опоры R₁ (нагрузку подставляем в [кН] а размеры в [м]):

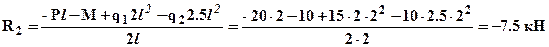
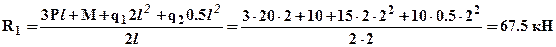
Для проверки правильности нахождения реакций составим еще одно уравнение равновесия:

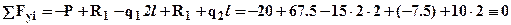. Найденные реакции удовлетворяют этому условию, следовательно, реакции определены верно.

3). Построим эпюры перерезывающих сил - Q и изгибающих моментов - M по участкам балки, используя метод сечений в следующей последовательности:

- в пределах каждого участка проводим произвольное поперечное сечение на расстоянии x_i от начала координат, (которое выбирается, как правило, в центре тяжести крайнего левого сечения балки) затем любая (в нашем случае правая) часть балки отбрасывается;

- отброшенная часть заменяется внутренними силовыми факторами Q и M (т.е. внутренними силами взаимодействия частей балки, которые можно считать реакциями отброшенной части);

- силовые факторы Q и M определяются из условий равновесия оставшейся части, при этом искомые силовые факторы всегда следует показывать в положительных направлениях, так чтобы изгибающий момент стремился сжимать верхние волокна, а перерезывающая сила стремилась вращать рассматриваемую часть по часовой стрелке.

Первый участок 0 £ x₁ £ l. Перерезывающую силу Q₁(x₁) найдем из уравнения для равновесия рассматриваемой части (смотри рис.1):

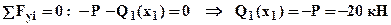- очевидно, что эпюрой будет горизонтальная прямая. Изгибающий момент M₁(x₁) найдем из уравнения для равновесия рассматриваемой части (см. рис.1): 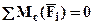(здесь и далее при определении изгибающих моментов в сечении в качестве моментной точки удобно выбирать центр тяжести рассматриваемого сечения) откуда:

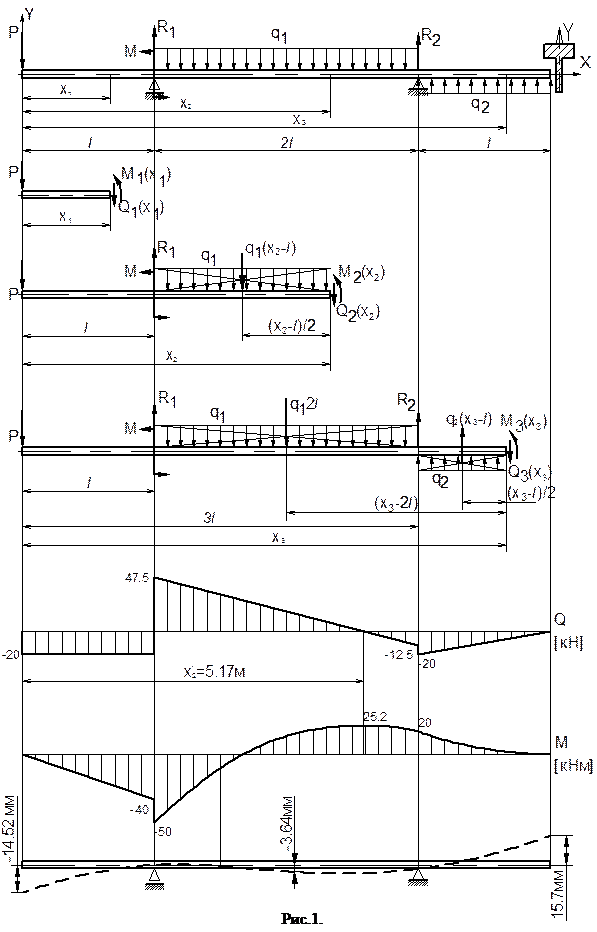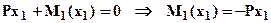. Зависимость M₁(x₁) – линейная, следовательно, эпюру можно построить по двум значениям на границах участка: 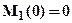и .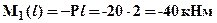

Второй участок l £ x₂ £ 3 l. Перерезывающую силу Q₂(x₂) найдем из уравнения равновесия для рассматриваемой части (смотри рис.1):

.

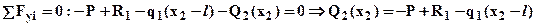Зависимость Q₂(x₂) – линейная, следовательно, эпюру строим по двум значениям на границах: 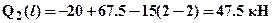и . И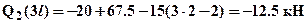згибающий момент M₂(x₂) найдем из уравнения для равновесия рассматриваемой части (распределенную нагрузку при этом заменяем равнодействующей см. рис.1):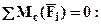 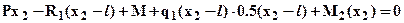, откуда следует:

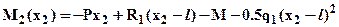. Зависимость M₂(x₂) – квадратичная, эпюра соответственно парабола, следовательно, кроме значений на границах участка:

;

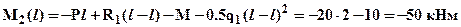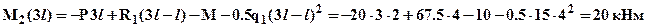требуется определить значение момента в вершине параболы. Координату вершины параболы - 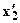найдем как точку экстремума из условия: 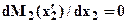. Согласно дифференциальной зависимости: 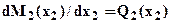, значит, 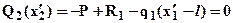откуда определим: 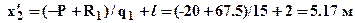. Вычислим значение

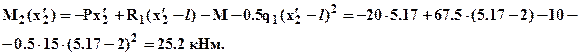
По рассчитанным трем значениям моментов строим эпюру изгибающего момента на втором участке (см. рис.1).

Третий участок 3 l £ x₃ £ 4 l. Перерезывающую силу Q₃(x₃) найдем из уравнения для равновесия рассматриваемой части (смотри рис.1):

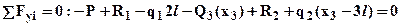откуда выразим перерезывающую силу - 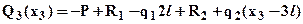. Зависимость Q₃(x₃) – линейная, следовательно, эпюру строим по двум значениям на границах:

.

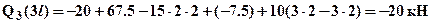
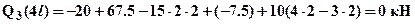Изгибающий момент M₃(x₃) найдем из уравнения равновесия 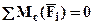, рассматриваемой части (распределенные нагрузки при этом заменяем равнодействующими см. рис.1):

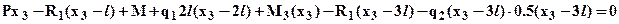, откуда: 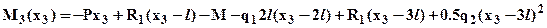. Зависимость M₃(x₃) – квадратичная, эпюра моментов парабола, следовательно, кроме значений на границах участка:

;

,

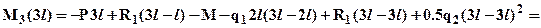
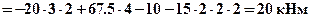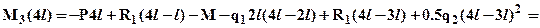
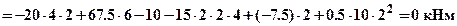требуется определить значение момента в вершине параболы. Однако, используя дифференциальную зависимость 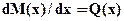легко определить, что вершина эпюры моментов совпадает с правой границей участка (x₃ = 4 l), так как в этом сечении Q₃(x₃)=0. Значит, эпюру можно построить по значениям на границах участка, учитывая, что выпуклость эпюры моментов всегда направлена навстречу направлению распределенной нагрузки на участке (см. рис.1).

После построения эпюр Q и M нужно выполнить их качественную проверку по дифференциальным зависимостям: по первой зависимости - 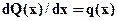можно проверить построение эпюры перерезывающей силы по приложенной (или отсутствующей) распределенной нагрузке; по второй зависимости - 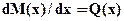можно проверить построение эпюры изгибающего момента по эпюре перерезывающей силы. Кроме того, следует учитывать следующие правила: в сечениях, где приложена сосредоточенная сила, на эпюре Q имеет место разрыв (скачек) на величину приложенной силы; в сечениях, где приложен сосредоточенный момент, на эпюре M имеет место разрыв (скачек) на величину приложенного момента.

4). Для заданного поперечного сечения балки (рис.2)

определим положение нейтральной линии. Как известно, нейтральная линия совпадает главной центральной осью перпендикулярной грузовой плоскости, в нашем случае грузовой плоскостью является - XY, следовательно, нейтральная линия совпадает с осью Z_c. Выберем начальную систему координат как показано на рис.2. Разобьем сечение на простейшие фигуры – два прямоугольника верхний и нижний с площадями соответственно: 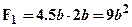и 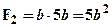. 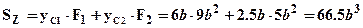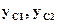Вычислим статический момент сечения относительно начальной оси Z как сумму статических моментов верхнего и нижнего прямоугольников где: соответственно координаты центров тяжести верхнего и нижнего прямоугольника. Положение нейтральной линии (оси Z_c) определится координатой 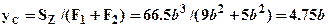. 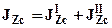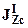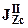Определим момент инерции сечения относительно нейтральной линии (оси Z_c): , где - и соответственно моменты инерции верхнего и нижнего прямоугольников:

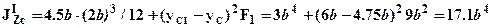
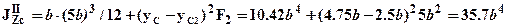
первые слагаемые в приведенных выражениях есть моменты инерции верхнего и нижнего прямоугольников относительно собственных центральных осей (параллельных оси Z_c), вторые слагаемые являются поправками Штейнера для перехода от собственных центральных осей прямоугольников к оси Z_c. Таким образом, момент инерции сечения относительно нейтральной линии Z_c: .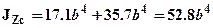

Вычислим моменты сопротивления сечения для верхних и нижних волокон:

; ,

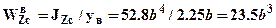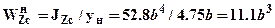где 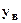, 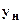соответственно расстояния от нейтральной линии до крайних верхних и крайних нижних волокон (см. рис.2).

5).Из условия прочности по нормальным напряжениям определим минимально необходимый размер поперечного сечения – b. Определим сначала опасные с точки зрения прочности сечения. Потенциально опасными будут сечения с наибольшим положительным 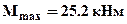и наибольшим отрицательным 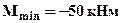изгибающими моментами, так как поперечное сечение стержня несимметрично относительно нейтральной линии и материал стержня имеет разные допускаемые напряжения на растяжение и сжатие (в других случаях, если хотя бы одно из этих условий не выполняется, то опасным будет сечение с наибольшим по модулю моментом). В каждом из этих сечений опасными могут оказаться точки наиболее удаленные от нейтральной линии, то есть крайние верхние или крайние нижние волокна. В самом общем случае для двух опасных сечений следует рассмотреть четыре условия прочности.(Все расчеты прочности и жесткости в дальнейшем удобнее вести в размерностях: [Н]; [мм]; [МПа]).

Записывая условия прочности для сечения с 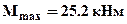для сжатых (верхних) волокон: ;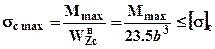

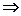
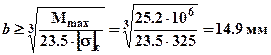для растянутых (нижних) волокон:

.

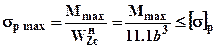
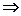
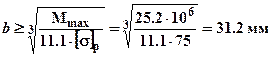Из условия прочности для сечения с 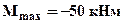для растянутых (верхних) волокон (в формулах для расчета напряжений изгибающий момент всегда берется по модулю а знак напряжений определяется характером деформации соответствующих волокон): ;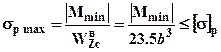

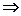
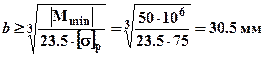для сжатых (нижних) волокон:

.

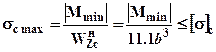
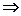
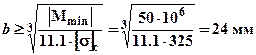Максимальное значение - 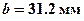получилось из условия прочности растянутых (нижних) волокон сечения с моментом 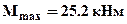, значит самыми опасными являются эти волокна. Окончательно принимаем - .

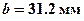Для проверки рассчитаем действующие в опасных напряжения и убедимся, что условия прочности выполнены. Для сечения с моментом 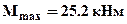: в верхних волокнах напряжения сжатия – 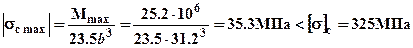; в нижних волокнах напряжения растяжения – .

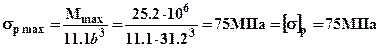Для сечения с моментом 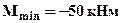: в верхних волокнах напряжения растяжения – 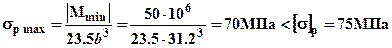; в нижних волокнах напряжения сжатия – 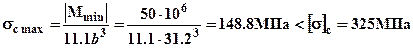. По полученным значениям строим эпюры нормальных напряжений в опасных сечениях (см. рис.2). Определим величину момента инерции сечения относительно оси Z_c:

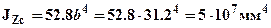
6).Выполним проверку прочности балки. Напряженное состояние в сечениях балки при поперечном изгибе является плоским и в прочностных расчетах в общем случае следует использовать теории прочности. Однако, в рассматриваемом примере сечение не является тонкостенным и следовательно касательные напряжения малы по сравнению с нормальными, кроме того большие по величине нормальные и касательные напряжения действуют в разных точках сечения (см. эпюры рис.2). Учитывая изложенное выше, проверку прочности можно свести к условию прочности отдельно по касательным напряжениям.

Допускаемые касательные напряжения ориентировочно можно определить как: 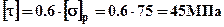. Для расчета касательных напряжений в поперечном сечении используем формулу Журавского: 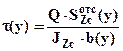, где 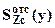- статический момент отсеченной части (лежащей выше или ниже линии с координатой y, на которой определяются напряжения t) сечения относительно оси Z_c. Формула Журавского выведена в предположении, что касательные напряжения направлены по оси Y и постоянны по ширине сечения. Максимальные касательные напряжения возникают в сечении с 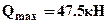. Для сечения любой формы статический момент отсеченной части максимален на нейтральной линии: 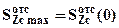, в рассматриваемом сечении на той же линии ширина сечения минимальна и равна 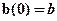, следовательно 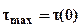. Удобно вычислить 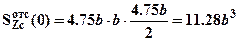как статический момент прямоугольника расположенного ниже Z_c. Тогда, 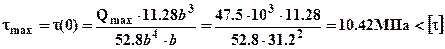условие прочности по касательным напряжениям выполняется. Для построения эпюры касательных напряжений в опасном сечении (см. рис.2) учтем, что на крайних волокнах верхних и нижних касательные напряжения всегда равны нулю, так как для них 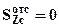(нет отсеченной части). Кроме того, по формуле Журавского вычислим касательные напряжения на границе верхнего и нижнего прямоугольников при 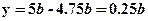: 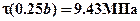- для ширины 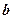и соответственно в 4.5 раза меньше 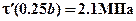- для ширины .

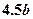Эпюра t(y) для верхнего прямоугольника условна и показана штрихами, так как ширина прямоугольника больше его высоты и формула Журавского здесь применима только для ориентировочных расчетов.

7).Запишем уравнение изогнутой оси балки, используя общие выражения метода начальных параметров, учитывая направление нагрузок показанное на рис.1:

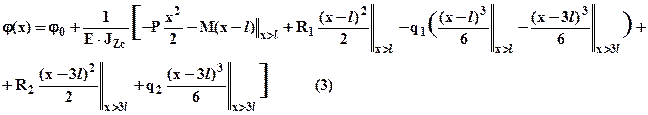- уравнение углов поворота поперечных сечений;

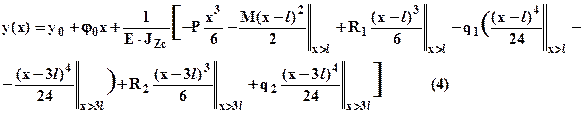
уравнение прогибов поперечных сечений. При определении прогибов или углов поворота в произвольном сечении с координатой - x в вышеприведенных уравнениях удерживаются только те слагаемые, которые учитывают нагрузки, приложенные к балке левее рассматриваемого сечения. Двойные черточки у слагаемых показывают, при каком условии данное слагаемое включается в вычисления.

Начальные параметры - 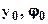имеют смысл соответственно прогиба и угла сечения находящегося в начале координат (при x = 0), и должны быть определены из граничных условий. В качестве граничных условий используем тот факт что прогибы сечений где расположены опоры равны нулю, которые могут быть записаны: 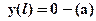; 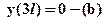. Подставляя условие (а) в выражение (4) получим следующее уравнение:

.

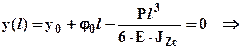
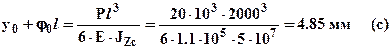Подставляя условие (b) в выражение (4) получим соответственно:

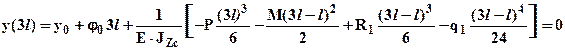
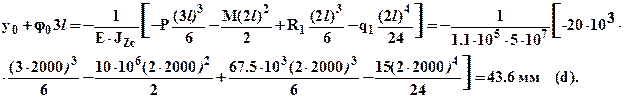
Решая совместно уравнения (c), (d) определяем: 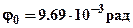и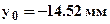

Теперь, когда определены начальные параметры 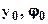по формулам (3) и (4) можно определить угол поворота и прогиб любого сечения балки. Определим, например, прогиб среднего сечения второго участка (x = 2 l):

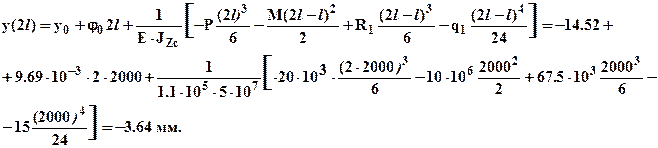Кроме того, определим прогиб крайнего правого сечения балки (x = 4 l):

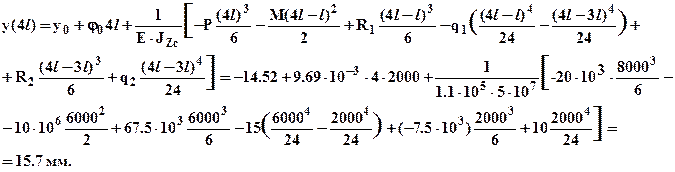По рассчитанным прогибам можно построить приблизительную форму изогнутой оси балки смотри рис.1. При этом следует учитывать, что выпуклость изогнутой оси направлена вверх, если изгибающий момент отрицательный, а при положительном изгибающем моменте выпуклость изогнутой оси направлена вниз.

8). Определим перемещения сечения 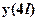и угол поворота сечения 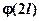и энергетическим способом, а именно способом Верещагина.

Сначала определим сначала 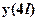, для этого приложим в искомом сечении единичную силу см. рис.3. Определим реакции опор, используя уравнения равновесия всей балки: из суммы моментов относительно опоры левой получим – 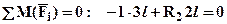, откуда 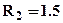, из 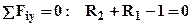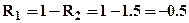. Строим эпюру единичного изгибающего момента (от действия только единичной нагрузки) по тем же правилам что и грузовую, описание построения эпюры опускаем в силу элементарности. Единичная эпюра представлена на рис.3, там же для удобства повторена эпюра грузового момента с обозначенными площадями участков и положением их центров тяжести (участки эпюры разбиты на простейшие фигуры для удобства определения площадей и центров тяжести). Теперь для определения 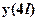нужно перемножить эпюры 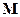и 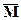по формуле Верещагина: 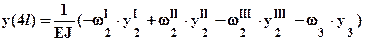, отрицательный знак означает, что

участок грузовой эпюры и единичная эпюра лежат на разноименных волокнах. Вычисляя

площади треугольника - 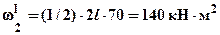, прямоугольника –

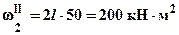, симметричной (относительно середины участка) параболы - 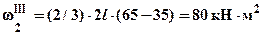, криволинейного треугольника (парабола с вершиной на правой границе) - 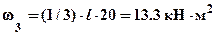. Кроме того, на рис.3 показаны ординаты единичного момента в сечениях, где находятся центры тяжестей соответствующих участков эпюры грузового момента, значения которых - 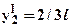, , 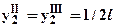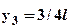. Подставляя значения в формулу Верещагина (в размерностях – Н, МПа, мм) получим: 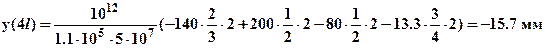, знак «-» означает, что перемещение направлено против направления единичной силы, то есть вверх. Таким образом, результат совпадает с полученным ранее.

Для определения 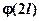к балке в сечении x=2l приложим единичный момент (см. рис.4). Составляя уравнение равновесия относительно левой опоры 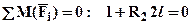Þ 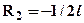, а из условия 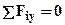очевидно, что 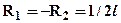. Эпюра единичного момента совместно с грузовой эпюрой представлена на рис.4. Для использования формулы Верещагина грузовую эпюру на втором участке необходимо разбить еще на 2 участка (соответственно единичной) каждый из которых ограничен квадратичной параболой. Вычисление площадей и центров тяжести грузовой эпюрой в этом случае весьма трудоемкая задача и для перемножения эпюр по Верещагину рационально использовать формулу Симпсона-Корноухова, на рис. 4 проставлены необходимые для перемножения

ординаты эпюр – значения ординат на границах и серединах участков.

Применяя формулу Симпсона-Корноухова для значения в (в размерностях – Н, МПа, мм) получим следующий результат:

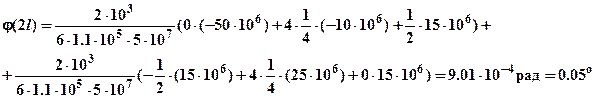
Знак «+» означает, что сечение поворачивается по направлению единичного момента против часовой стрелки.