Задача №1. Задание: для заданной стальной балки с поперечным сечением в виде двутаврового профиля нагруженной в плоскости XY (рис. 1) из условия прочности подобрать

Задание: Для заданной стальной балки с поперечным сечением в виде двутаврового профиля нагруженной в плоскости XY (рис.1) из условия прочности подобрать величину допускаемой внешней нагрузки [q]. При найденной нагрузке определить перемещения некоторых про­извольных сечений балки двумя способами: а) используя дифференциальное уравнение упругой линии; б) энергетическим методом.

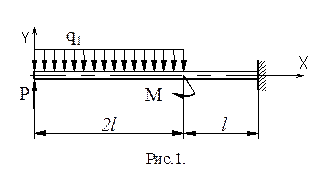Исходные данные: l = 1.5 м; P = 1.5q l; М = 2q l²; q₁ = 2q. Сечение балки двутавр №27 по ГОСТ 8239 –72. Материал балки Сталь30, с модулем продольной упругости (модулем Юнга) - Е=2×10⁵ МПа и пределом текучести s_т = 300 МПа.

Решение:

1).Определим допускаемые напряжения для материала стержней на растяжение и сжатие, коэффициент запаса прочности, учитывая что материал балки относительно пластичный, примем: n=1.5: .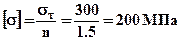

2).Заменим жесткую заделку ее реакциями (см. рис.2.) и определим их из условий равновесия всей балки: из суммы моментов относительно жесткой заделки получим – 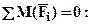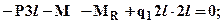откуда ,

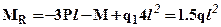а из суммы моментов относительно начального (крайнего левого) сечения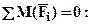

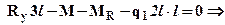
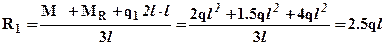. Для проверки правильности нахождения реакций составим еще одно уравнение равновесия:

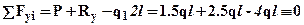. Найденные реакции удовлетворяют этому условию, следовательно, реакции определены верно.

3). Построим эпюры перерезывающих сил - Q и изгибающих моментов - M по участкам балки, используя метод сечений в следующей последовательности:

- в пределах каждого участка проводим произвольное поперечное сечение на расстоянии x_i от начала координат, (которое выбирается, как правило, в центре тяжести крайнего левого сечения балки) затем любая (в нашем случае правая) часть балки отбрасывается;

- отброшенная часть заменяется внутренними силовыми факторами Q и M (т.е. внутренними силами взаимодействия частей балки, которые можно считать реакциями отброшенной части);

- силовые факторы Q и M определяются из условий равновесия оставшейся части, при этом искомые силовые факторы всегда следует показывать в положительных направлениях, так чтобы изгибающий момент стремился сжимать верхние волокна, а перерезывающая сила стремилась вращать рассматриваемую часть по часовой стрелке.

Первый участок 0 £ x₁ £ 2 l. Перерезывающую силу Q₁(x₁) найдем из уравнения для равновесия рассматриваемой части (смотри рис.2):

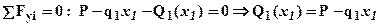или .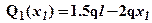

Зависимость Q₁(x₁) – линейная, следовательно, эпюру строим по двум значениям на границах: 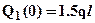и . И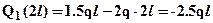згибающий момент M₁(x₁) найдем из уравнения для равновесия рассматриваемой части (распределенную нагрузку при этом заменяем равнодействующей см. рис.2):

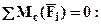
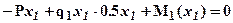, (здесь и далее при определении изгибающих моментов в сечении в качестве моментной точки удобно выбирать центр тяжести рассматриваемого сечения) откуда следует:

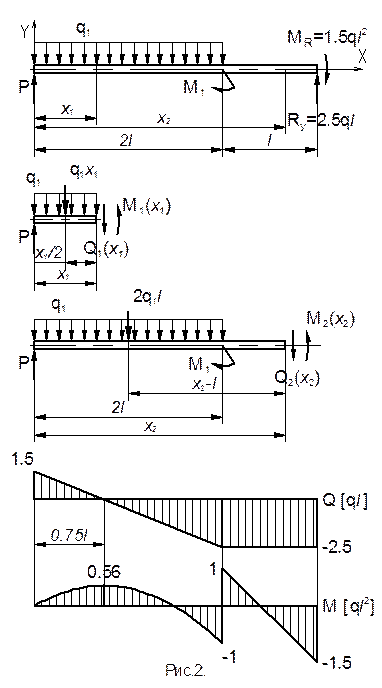
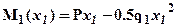
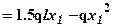. Зависимость M₁(x₁) – квадратичная, эпюра соответственно парабола, следовательно, кроме значений на границах участка: 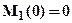; 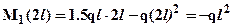, требуется определить значение момента в вершине параболы. Координату вершины параболы - 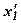найдем как точку экстремума из условия: 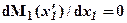. Согласно известной дифференциальной зависимости:

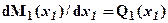, тогда из условия 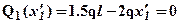определим: .

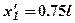Вычислим значение 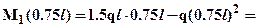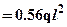. Кроме того, в дальнейшем для определения перемещений энергетическим методом нам понадобится значение момента посередине участка 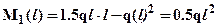. По рассчитанным значениям моментов строим эпюру изгибающего момента и перерезывающей силы на первом участке (см. рис.2).

Второй участок 2 l £ x₂ £ 3 l. Перерезывающую силу Q₂(x₂) найдем из уравнения для равновесия рассматриваемой части (смотри рис.2):

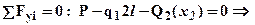
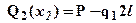
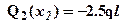- очевидно, что эпюрой будет горизонтальная прямая. Изгибающий момент M₂(x₂) найдем из уравнения равновесия рассматриваемой части (см. рис.2):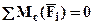

откуда: 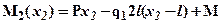или окончательно 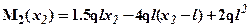. Зависимость M₂(x₂) – линейная, следовательно, эпюру можно построить по двум значениям на границах участка: 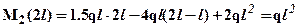; 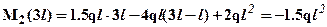. Снова для определения перемещений энергетическим методом определим значение момента посередине участка - .

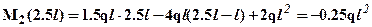По рассчитанным значениям моментов строим эпюру изгибающего момента и перерезывающей силы на первом участке (см. рис.2).

После построения эпюр Q и M нужно выполнить их качественную проверку по дифференциальным зависимостям: по первой зависимости - 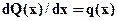можно проверить построение эпюры перерезывающей силы по приложенной (или отсутствующей) распределенной нагрузке; по второй зависимости - 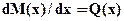можно проверить построение эпюры изгибающего момента по эпюре перерезывающей силы. Кроме того, следует учитывать следующие правила: в сечениях, где приложена сосредоточенная сила, на эпюре Q имеет место разрыв (скачек) на величину приложенной силы; в сечениях, где приложен сосредоточенный момент, на эпюре M имеет место разрыв (скачек) на величину приложенного момента.

4). Для заданного поперечного сечения балки выпишем из сортамента необходимые геометрические характеристики: 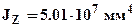- момент инерции сечения относительно нейтральной линии; 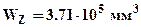- момент сопротивления сечения изгибу относительно нейтральной линии; 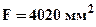- площадь поперечного сечения; 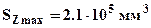- статический момент половины сечения относительно нейтральной линии; 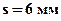- толщина стенки; 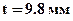- средняя толщина полки; h = 270 мм - высота сечения; b = 125 мм – ширина полок двутавра.

Из условия прочности по нормальным напряжениям определим допускаемую величину внешней нагрузки. Определим сначала опасные с точки зрения прочности сечения. Учитывая, что сечение симметрично относительно нейтральной линии (кроме того, материал имеет одинаковую прочность на растяжение и сжатие) опасным будет сечение с наибольшим по модулю моментом изгибающим моментам 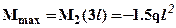. В этом сечении опасными будут точки наиболее удаленные от нейтральной линии, то есть крайние верхние или крайние нижние волокна. Записывая условия прочности для опасного сечения (все расчеты прочности и жесткости в дальнейшем удобнее вести в размерностях: [Н]; [мм]; [МПа]): получим допускаемое значение внешней нагрузки .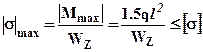

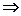
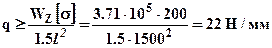5).Для сравнения определим при найденной величине внешней нагрузки подберем прямоугольное сечение с отношением сторон 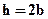, момент сопротивления изгибу для него 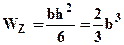. Записывая условие прочности для такого сечения 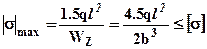откуда ширина - 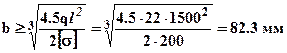, высота - 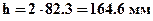, 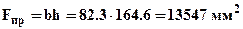. Тогда при одинаковой прочности расход материала на балку прямоугольного сечения будет в 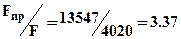раза больше чем на балку двутавровую.

6).Для балки двутаврового профиля выполним уточненную проверку прочности. Сечение балки является тонкостенным величина касательных напряжений в поперечных сечениях может оказаться сравнимой с величиной нормальных напряжений. Таким образом, 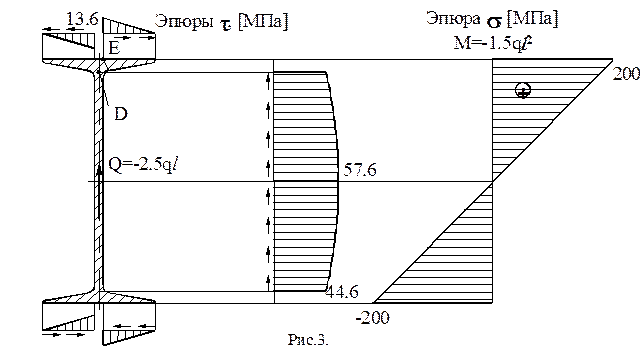напряженное состояние балки при поперечном изгибе является существенно двумерным (плоским) и при проверке прочности следует воспользоваться одной из теорий прочности, например IV-ой теорией. Опасными сечениями могут оказаться сечения, в которых одновременно действуют большие по величине Q и M. В рассматриваемом примере очевидно, что опасным является сечение в заделке x₂=3l где действуют одновременно максимальные по модулю перерезывающая сила и изгибающий момент (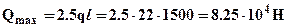, 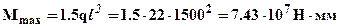) и следовательно возникают наибольшие нормальные и касательные напряжения. Эпюра нормальных напряжений в опасном сечении показана на рис.3. Для расчета касательных напряжений в тонкостенном сечении применима формула Журавского: 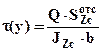, где 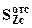- статический момент отсеченной части сечения относительно оси нейтральной линии. В тонкостенных сечениях касательные напряжения считаются направленными параллельно средней линии сечения (которая делит толщину стенки (полки) пополам), и постоянными по толщине. Эпюра касательных напряжений в сечении показана на рис.3. Направления касательных напряжений в стенке и полках двутавра зависят от направления перерезывающей силы и показаны на том же рисунке стрелками. Для построения эпюры касательных напряжений достаточно вычислить их значения в трех точках сечения. В расчетах обычно полки переменной толщины заменяются прямоугольниками с размерами 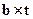. Максимальные касательные напряжения возникают на нейтральной линии, где наибольший статический момент отсеченной части сечения и минимальная толщина сечения равная - s:

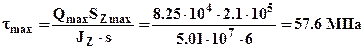. Для определения касательных напряжений в стенке в месте соединения с полкой - 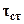, необходимо вычислить статический момент площади полки относительно нейтральной линии сечения: .

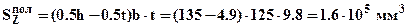Тогда .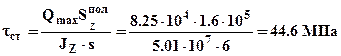

Максимальные касательные напряжения в полках равны .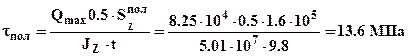

По эпюрам нормальных и касательных напряжений представленным на рис.3 видно, что опасными точками в сечении являются т. D и E. Определим в этих точках эквивалентные напряжения по IV-ой теории прочности. Эквивалентное напряжение в т.D 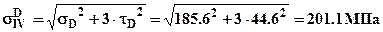, нормальное напряжение 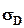можно определить графически по эпюре рис.3 или используя общую формулу 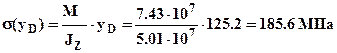, где 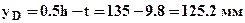- расстояние от нейтральной линии до точки D. Эквивалентное напряжение в т.E 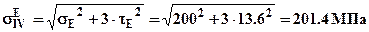. Эквивалентные напряжения в опасных точках превосходят допускаемые 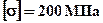, однако перегрузка составляет < 5% и прочность балки можно считать обеспеченной. В случаях, когда максимальные напряжения превосходят допускаемые более чем на 5% для выполнения условий прочности следует пропорционально уменьшить нагрузку или увеличить размеры сечения.

7).Запишем и решим дифференциальное уравнение упругой линии для рассматриваемой балки. Балка состоит из двух участков и следовательно необходимо записать и проинтегрировать дифференциальные уравнения для каждого из них.

Первый участок - 0 £ x₁ £ 2 l: .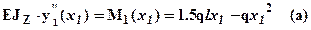

Интегрируя два раза, получим соответственно выражения для углов поворота и прогибов:

.

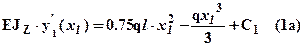
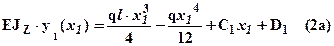Второй участок - 2 l £ x₁ £ 3 l: .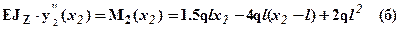

Интегрируя, получим выражения для углов поворота и прогибов для второго участка:

.

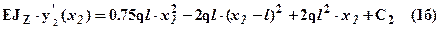
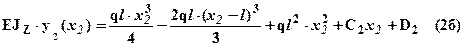Для определения 4-х констант интегрирования имеются 4 граничных условия. Два граничных условия должны учесть способ закрепления балки, то есть тот факт, что прогиб и угол поворота сечения в жесткой заделке равны нулю: 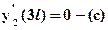; 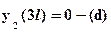. Два других граничных условия являются условиями неразрывности балки на границе между участками: 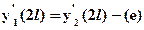; 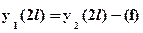. Поставляя уравнения 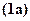и 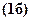в граничное условие 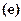, уравнения 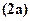и 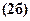в условие 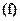, уравнение 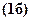в условие 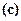, уравнение 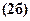в условие 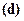получим следующую систему линейных уравнений относительно констант интегрирования:

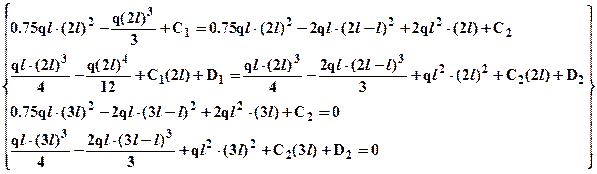
Упрощая и преобразуя запишем систему ее в виде:

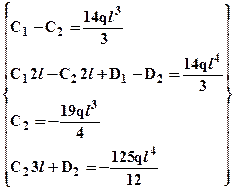
Разрешая последнюю систему, определяем неизвестные: 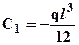; ; 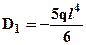; 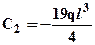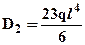. Теперь выражения для прогибов и углов поворота для обоих участков становятся полностью определенными и записываются в виде:

.

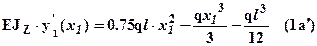
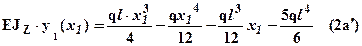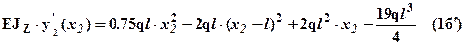
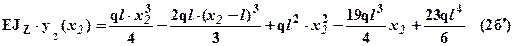. Используя эти выражения можно рассчитать прогиб и угол поворота любого сечения балки, например прогиб - 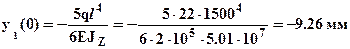и угол поворота –

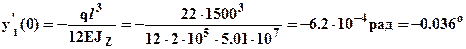крайнего левого сечения балки. Отрицательные значения прогиба означают, что прогиб направлен вниз, отрицательные значения угла поворота означают, что поворот сечения происходит по часовой стрелке. Отметим, что определение 4-х констант, несмотря на относительную простоту рассматриваемой балки, оказалось довольно трудоемкой процедурой, поэтому для определения перемещений рационально использовать метод начальных параметров. Использование метода начальных параметров для определения перемещений рассмотрено в задаче №2.

8). Снова определим прогиб и угол поворота крайнего левого сечения, но уже энергетическим методом используя интеграл Мора.

Согласно методу Мора для определения прогиба в сечении рассмотрим 1-е единичное состояние, приложим в сечении единичную вертикальную силу и построим эпюру единичного момента 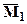см. рис.4. Далее интеграл Мора для прогиба данного сечения будем вычислять способом Верещагина, согласно которому необходимо перемножить эпюру грузового (изгибающего момента от внешней нагрузки) момента на соответствующую единичную 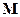´ 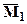. На рис.4 для наглядности перенесена эпюра грузового момента построенная ранее (рис.2). Так как вычисление центров тяжести и площадей участков грузовой эпюры в данном случае достаточно трудоемко воспользуемся формулой Симпсона-Корноухова. На рис.4 показаны ординаты единичной и грузовой эпюр на левой и правой границах и в средних сечениях каждого участка, необходимые для формулы Симпсона-Корноухова. Подставляя необходимые значения с эпюр в формулу Симпсона-Корноухова, получим искомый прогиб сечения:

.

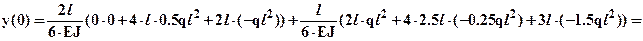
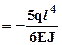Для определения угла поворота крайнего левого сечения рассмотрим 2-е единичное состояние, приложим в сечении единичный момент. Построим эпюру единичного момента 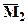см. рис.4. Перемножая эпюры 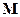´ 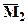по Верещагину, снова используем формулу Симпсона-Корноухова. Подставляя необходимые значения с эпюр в формулу Симпсона-Корноухова, получим угол поворота сечения:

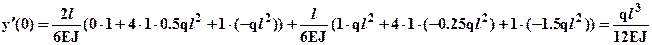Найденные значения совпадают по модулю с полученными при решении дифференциального уравнения упругой линии. В энергетических методах знак «+» означает, что направление перемещения совпадает с направлением соответствующей единичной нагрузки, знак «-» означает, что направление перемещения противоположно направлению единичной нагрузки. Следовательно в рассматриваемом случае прогиб сечения направлен вниз, а поворот сечения происходит по направлению единичного момента (см.рис.4) то есть по часовой стрелке. Таким образом направления перемещений совпадают с полученными при решении дифференциального уравнения упругой линии, что является подтверждением правильности определения перемещений.