Пусть 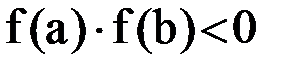 , а
, а 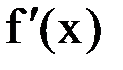 и
и 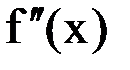 сохраняют постоянные знаки на отрезке
сохраняют постоянные знаки на отрезке 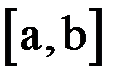 . Соединяя методы хорд и касательных, получаем метод на каждом этапе, которого находим значения по недостатку и значения по избытку точного корня
. Соединяя методы хорд и касательных, получаем метод на каждом этапе, которого находим значения по недостатку и значения по избытку точного корня 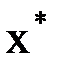 уравнения
уравнения 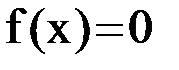 . Пусть
. Пусть 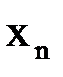 – последовательные приближения метода хорд,
– последовательные приближения метода хорд, 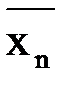 – последовательные приближения метода касательных. Пошаговая иллюстрация представлена на рисунке 11.
– последовательные приближения метода касательных. Пошаговая иллюстрация представлена на рисунке 11.
Возможны 4 случая: 1) 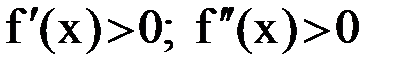 , 2)
, 2) 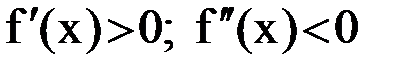 ,
,
3) 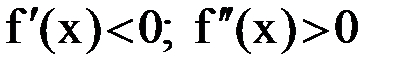 , 4)
, 4) 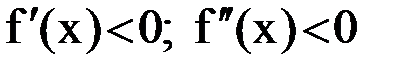 ,
,
которые можно свести к первому случаю.
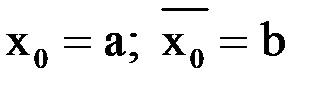 .
.
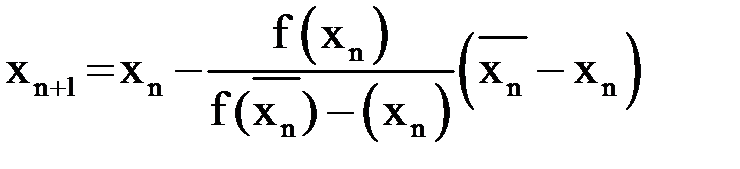 .
. 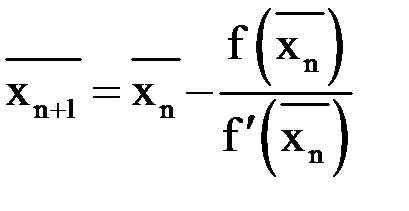 .
.
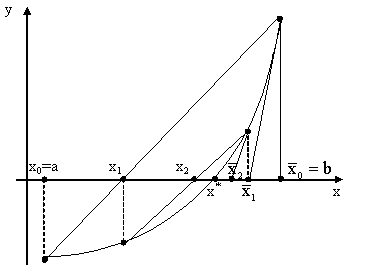
Рисунок 1.10 – Последовательные приближение методом
касательных
Очевидно, что 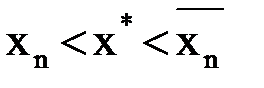 и
и 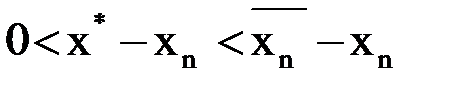 .
.
По окончании процесса за значение корня 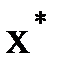 лучше всего взять среднее арифметическое полученных значений:
лучше всего взять среднее арифметическое полученных значений: 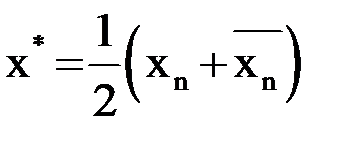 .
.
Пример 1.4. Вычислить положительный корень уравнения 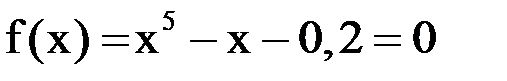 . Так как
. Так как 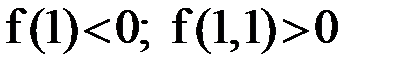 , то
, то 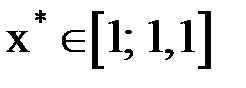 .
.
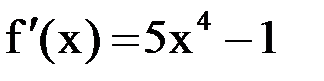 ,
, 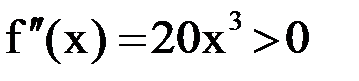 на
на 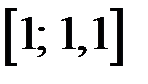 , поэтому
, поэтому 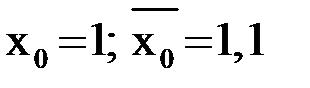 .
.
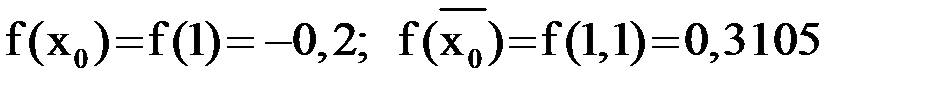 .
.
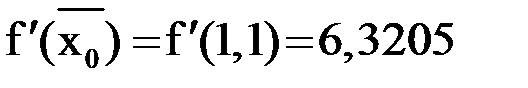 .
.
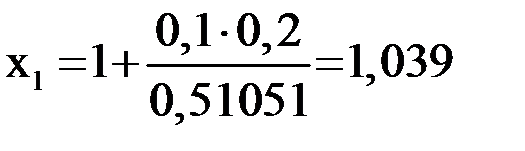 ;
; 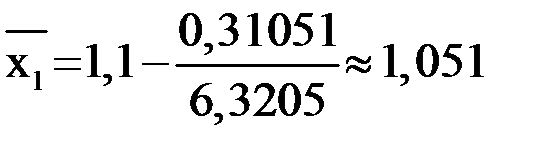 .
.
Так как 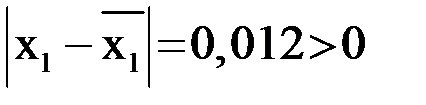 , то
, то
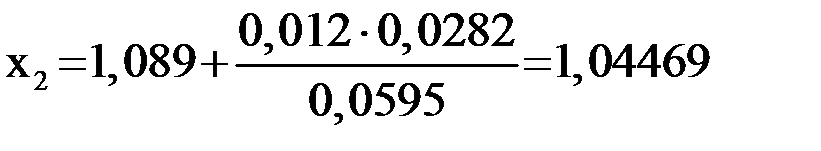 ;
; 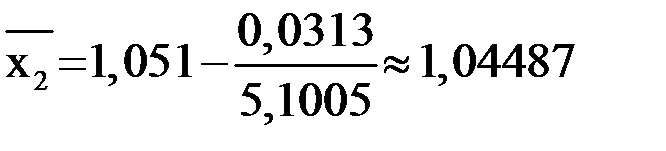 .
.
Так как 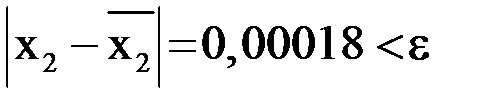 , то
, то 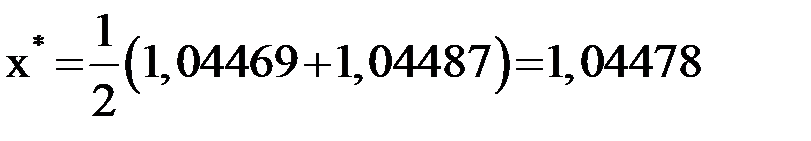 .
.
2 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
 2015-02-27
2015-02-27 444
444








