Требуется найти решение системы линейных уравнений:
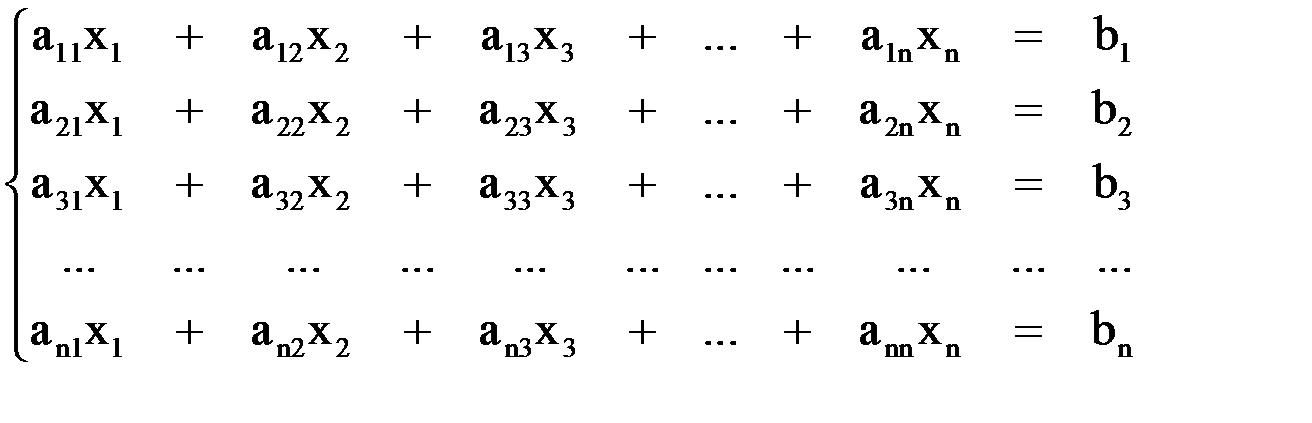
или в матричной форме: 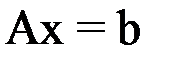 , где
, где
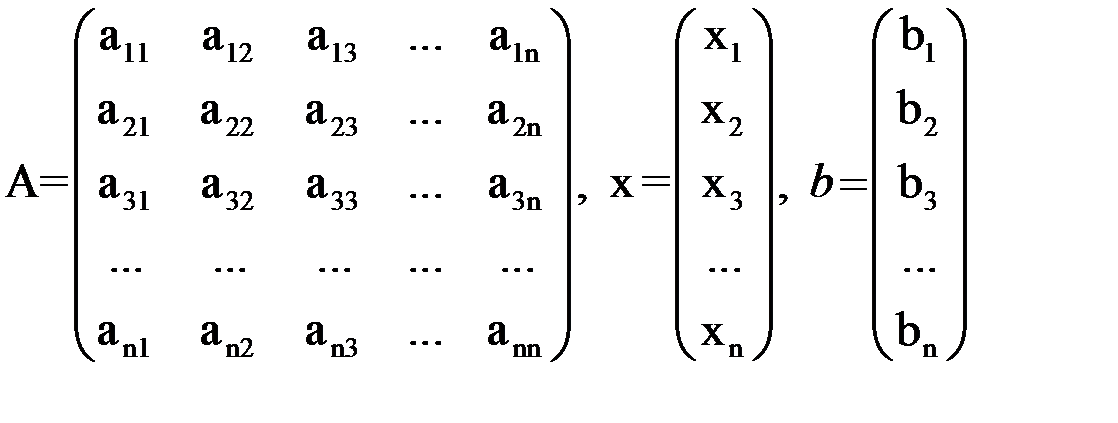
По правилу Крамера система 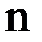 линейных уравнений имеет единственное решение, если определитель системы отличен от нуля
линейных уравнений имеет единственное решение, если определитель системы отличен от нуля 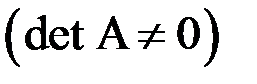 и значение каждого из неизвестных определяется следующим образом:
и значение каждого из неизвестных определяется следующим образом: 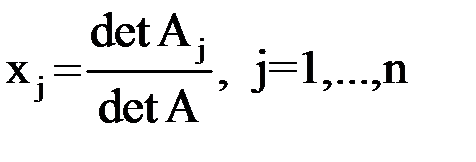 , где
, где 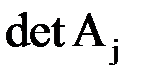 – определитель матрицы, получаемой заменой
– определитель матрицы, получаемой заменой 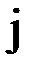 -го столбца матрицы
-го столбца матрицы 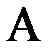 столбцом правых частей
столбцом правых частей 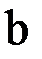 .
.
Непосредственный расчет определителей для больших 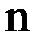 является очень трудоемким.
является очень трудоемким.
Известные в настоящее время многочисленные приближенные методы решения систем линейных алгебраических уравнений распадаются на две большие группы: прямые методы и методы итераций.
Прямые методы всегда гарантируют получение решения, если оно существуют, однако, для больших 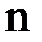 требуется большое количество операций, и возникает опасность накопления погрешностей.
требуется большое количество операций, и возникает опасность накопления погрешностей.
Этого недостатка лишены итерационные методы, но зато они не всегда сходятся и могут применяться лишь для систем определенных классов.
Норма матрицы является некоторой обобщенной оценкой значений элементов матрицы. Для её вычисления можно использовать следующие выражения:
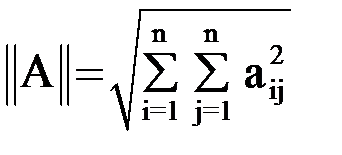 ,
,
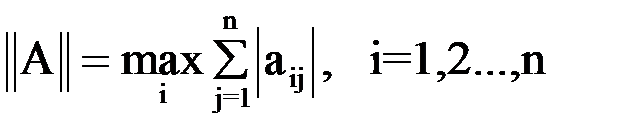 ,
, 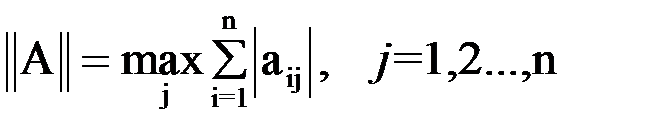 .
.
 2015-02-27
2015-02-27 367
367








