Таблица 7.
Расчеты при дисперсионном анализе однофакторных
комплексов для малых групп.
Градации (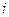 ) изучаемого фактора
– типы конституции ) изучаемого фактора
– типы конституции
| Число градаций (n=5) | ||||
| Грубый | Нежный | Плотный | Рыхлый | ||
| Варианты (число ягнят) - х | |||||
Число вариант – 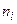
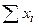
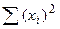
| N = 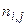 = 20 = 20
| ||||
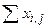 =37 =37
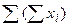 =368 =368
| |||||
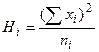
| 12,8 | 16,2 | 38,8 | 9,8 | 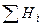 =72,6 =72,6
|
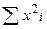
| 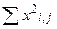 =77 =77
|
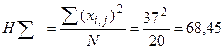
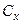 – факториальная (межгрупповая) дисперсия, характеризующая влияние изучаемого фактора (типа конституции овец), вычисляется по формуле:
– факториальная (межгрупповая) дисперсия, характеризующая влияние изучаемого фактора (типа конституции овец), вычисляется по формуле:
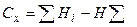
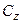 – случайная, остаточная (внутригрупповая) дисперсия, обусловленная влиянием всех других факторов, вычисляется по формуле:
– случайная, остаточная (внутригрупповая) дисперсия, обусловленная влиянием всех других факторов, вычисляется по формуле:
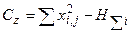
Величины дисперсии составляют: 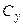 = 77 - 68,45 = 8,55;
= 77 - 68,45 = 8,55; 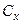 = 72,6 – 68,45 = 4,15;
= 72,6 – 68,45 = 4,15; 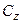 = 77-72,6 = 4,4.
= 77-72,6 = 4,4.
Таким образом, показатель общего разнообразия (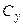 ) разложен на два составляющих компонента: разнообразие, зависящее от изучаемого фактора (типа конституции овец –
) разложен на два составляющих компонента: разнообразие, зависящее от изучаемого фактора (типа конституции овец – 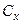 ) и разнообразие, зависящее от совокупности других факторов (
) и разнообразие, зависящее от совокупности других факторов (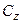 ). При этом, конечно,
). При этом, конечно, 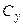 =
= 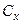 +
+ 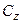 . В данном примере 8,55 = 4,15 +4,4 (целесообразно сделать подсчет для проверки правильности вычислений).
. В данном примере 8,55 = 4,15 +4,4 (целесообразно сделать подсчет для проверки правильности вычислений).
Для оценки доли общего разнообразия признака, обусловленной изучаемым фактором (типом конституции овец), выполняют отношение факториальной дисперсии. Это отношение обозначается символом 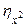 .
.
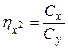
В разбираемом примере 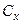 /
/ 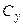 = 4,15: 8,55 = 0,49.
= 4,15: 8,55 = 0,49.
Следовательно, типом конституции обусловлено 49% общего разнообразия плодовитости овец.
Дисперсионный анализ позволяет оценить достоверность выводов. Для этого применяются три способа: вычисление средней ошибки силы влияния (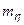 ), вычисление показателя достоверности влияния по Фишеру (F), вычисление показателя (
), вычисление показателя достоверности влияния по Фишеру (F), вычисление показателя (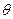 ) – показатель достоверности влияния по Н.А. Плохинскому. Третий, наиболее простой способ заключается в следующем: по данным опыта вычисляют эмпирический показатель
) – показатель достоверности влияния по Н.А. Плохинскому. Третий, наиболее простой способ заключается в следующем: по данным опыта вычисляют эмпирический показатель 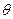 и сравнивают его со стандартным значением этого показателя (
и сравнивают его со стандартным значением этого показателя (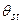 ), свидетельствующим о достоверности вывода с вероятностью 0,95. Стандартные значения
), свидетельствующим о достоверности вывода с вероятностью 0,95. Стандартные значения 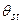 приведены в [3]. Вычисление эмпирического показателя достоверности производится по формуле:
приведены в [3]. Вычисление эмпирического показателя достоверности производится по формуле:
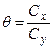
Чтобы найти стандартное значение 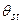 , нужно определить число степеней свободы (
, нужно определить число степеней свободы (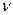 ). Для
). Для 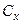 число степеней свободы
число степеней свободы 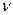 = r -1 (на единицу меньше числа градаций фактора х).
= r -1 (на единицу меньше числа градаций фактора х).
Для 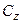 число степеней свободы равно общему числу вариант, уменьшенному на число градаций фактора:
число степеней свободы равно общему числу вариант, уменьшенному на число градаций фактора: 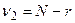 . Стандартные значения
. Стандартные значения 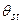 нужно найти в [3].
нужно найти в [3].
В рассматриваемом примере эмпирическое значение 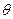 =
= 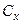 ;
; 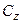 = 4,15/4,4 = 0,94; степени свободы равны:
= 4,15/4,4 = 0,94; степени свободы равны: 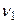 = 5 – 1 = 4;
= 5 – 1 = 4; 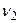 = 20 – 5 = 15. Согласно [3] находим:
= 20 – 5 = 15. Согласно [3] находим: 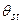 = 0,82 (среднее между 0,89 и 0,75). Эмпирическое значение
= 0,82 (среднее между 0,89 и 0,75). Эмпирическое значение 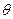 в данном случае выше стандартного, что свидетельствует о его достоверности с вероятностью более 0,95.
в данном случае выше стандартного, что свидетельствует о его достоверности с вероятностью более 0,95.
Задание № 11. Провести расчет однофакторного дисперсионного комплекса по содержанию жира в молоке дочерей отдельных быков – производителей (по Н.З. Басовскому стр. 116). Выявить силу влияния отдельных быков на жиромолочность.
Контрольные вопросы:
1. В чем заключается цель дисперсионного анализа?
2. Что называется общей, факториальной, остаточной дисперсией?
3. Какие бывают дисперсионные комплексы?
4. Как составляют однофакторный дисперсионный комплекс и вычисляют вспомогательные величины?
 2015-02-04
2015-02-04 553
553








