Для решения задач СТП переходят к детерминированному эквиваленту.
В Р-постановке для целевой функции детерминированный эквивалент имеет вид:
- при максимизации целевой функции (т.е. для задачи (6))
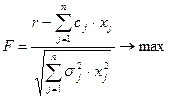
- при минимизации целевой функции (т.е. для задачи (7))
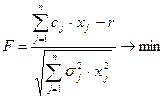
где 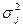 - дисперсия случайной величины
- дисперсия случайной величины 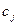 . Решение таких задач затруднительно, поэтому далее рассматриваем целевую функцию только в М-постановке.
. Решение таких задач затруднительно, поэтому далее рассматриваем целевую функцию только в М-постановке.
Детерминированный эквивалент вероятностного ограничения типа (1) может быть сведен к виду
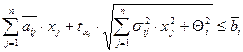
где 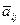 ,
, 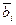 - математические ожидания;
- математические ожидания; 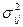 ,
, 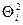 - дисперсии случайных величин
- дисперсии случайных величин 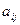 ,
, 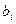 ;
; 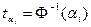 - обратная функция нормального распределения при функции распределения
- обратная функция нормального распределения при функции распределения
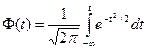
где 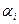 - заданный уровень вероятности (табл.):
- заданный уровень вероятности (табл.):
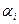 | 0,5 | 0,6 | 0,7 | 0,77 | 0,84 | 0,89 | 0,93 | 0,96 | 0,98 | 0,987 | 0,994 |
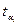 | 0,0 | 0,25 | 0,5 | 0,75 | 1,25 | 1,5 | 1,75 | 2,0 | 2,25 | 2,5 |
(Если же 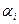 <0,5, то
<0,5, то 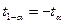 . Так, для
. Так, для 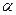 =0,4,
=0,4, 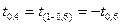 = -0,25.)
= -0,25.)
Детерминированный эквивалент задачи СТП в М-постановке, т.е. задачи (5), имеет вид:
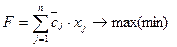 ;
;
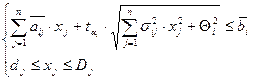 (8)
(8)
Каждое i-ое ограничение в детерминированном эквиваленте (8) отличается от аналогичного ограничения ЗЛП 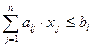 следующим:
следующим:
- от детерминированных значений 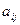 ,
, 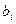 выполнен переход к математическим ожиданиям случайных величин
выполнен переход к математическим ожиданиям случайных величин 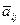 ,
, 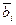 ;
;
- появился дополнительный член
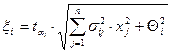 ,
,
который учитывает все вероятностные факторы: закон распределения с помощью 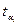 ; заданный уровень вероятности
; заданный уровень вероятности 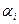 ; дисперсии случайных величин
; дисперсии случайных величин 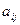 , равные
, равные 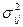 ; дисперсии случайных величин
; дисперсии случайных величин 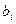 , равные
, равные 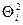 .
.
 2015-02-27
2015-02-27 1075
1075
