Непрерывно-детерминированные модели (D - схемы)

Непрерывно-детерминированные модели используются при описании и исследовании объектов, для которых отличительными характеристиками являются:

- отсутствие случайностей при работе и управлении объектом моделирования;

- явления в объектах моделирования рассматривают как непрерывные процессы, то есть те, в которых основная переменная, часто это время, является непрерывной величиной.

Модели построенные по этой схеме чаще всего ориентированы на изучение динамики рассматриваемого объекта (отсюда и название Д-схема). Поэтому характерным примером использования такого рода схемы являются дифференциальные уравнения.

Дискретно-детерминированная схема (F-схемы)

Для модели данного класса характерны два свойства, которые имеют доминирующее значение. Первым свойством моделей данного класса является полное отсутствие случайностей (детерминированность). Вторым свойством является рассмотрение явлений в объекте моделирования как изменяющихся во времени процессов, которые описываются соответствующими временными рядами (для них характерно пошаговое изменение времени, причем этот шаг определен и постоянен) - дискретно. Следовательно в отличие от D-схемы в F-схемах время описывается дискретной величиной. Для построения такого вида моделей используется чаще всего два инструмента: конечно-разностные уравнения и теория конечных автоматов.

Наиболее характерным примером применения дискретно – детерминированных схем является модель конечного автомата. Отсюда и название F-схемы - finite automat. Конечный автомат– это модель описания последовательности изменений состояния объекта, которые обусловлены его текущим состоянием и входным воздействием (возможное количество состояний автомата предполагается конечным). Обычно конечный автомат задают при помощи следующей совокупности множеств [75] [76]:

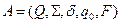
где:

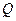· - конечное множество состояний автомата;

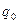· - начальное состояние автомата (;

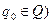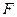· - множество заключительных состояний, ;

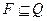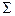· - конечное множество допустимых входных символов (входной алфавит);

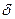· - функция переходов автомата: .

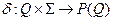Автомат функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют свои постоянные значения входного и выходного сигнала, а также внутреннего состояния автомата. Он начинает работу в состоянии q₀, считывая по одному из входных символов. После считывания автомат переходит в новое состояние из 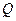в соответствии с функцией переходов. Если по завершении считывания входного слова (цепочки символов) автомат оказывается в одном из допустимых состояний, то слово «принимается» автоматом. В этом случае говорят, что оно принадлежит языку данного автомата. В противном случае слово «отвергается».

Дискретно-стохастические модели (Р-схемы)

Отличие этой схемы от F-схемы заключается в учете фактора случайности с позиций теории вероятности, т.е. она ориентирована на объекты, для которых характерно случайное поведение. Поскольку сущность дискретности основного параметра сохраняется, то основным представителем этой схемы является модель - вероятностного автомата (probabilistic automat) или P-автомата (отсюда и название: Р-схема).

Для построения математической модели вероятностного автомата необходимо описать законы распределения тех его сторон, которые характеризуются стохастичностью. Обычно это вероятности перехода из одного возможного состояния в другое. Более подробно с вероятностными автоматами можно познакомиться в работе [77] К дискретно-стохастической схеме можно отнести и цепи Маркова, которые моделируют в измеримом пространстве дискретный по времени и значению заданный марковский процесс. Напомним, что процесс является марковским, если он описывает такую последовательность случайных событий (событием является переход из одного состояния в другое в результате случайного испытания), в которой вероятность каждого события зависит только от состояния, в котором объект моделирования находится в текущий момент и не зависит от более ранних состояний. Поэтому конечная марковская цепь может быть задана полным множеством возможных состояний объекта 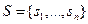и матрицей переходных вероятностей 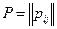, где 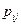есть вероятность перехода объекта из состоя 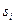в состояние 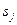, (предполагается, что вначале система может находиться в любом из возможных состояний с известной вероятностью ).

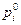Непрерывно-стохастические модели (Q-схемы)

Непрерывно-стохастические схемы отличаются непрерывным характером изменения времени и наличием случайности в поведении. Основной непрерывно-стохастической схемой формализованного описания служит аппарат систем массового обслуживания (queuing system).

В общем случае модель системы массового обслуживания (СМО) задается следующей совокупностью множеств[78]:

,

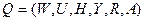где

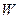- поток заявок;

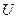- поток обслуживания (описание интервалов времени между началом и окончание обслуживанием заявки;

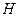- накопитель заявок;

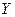- выходной поток;

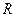- оператор сопряжения, отражающий взаимосвязь каналов и накопителей;

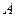- множество операторов поведения заявок

Когда говорят о СМО, подразумевают [79], что есть типовые пути (каналы обслуживания), через которые в процессе обработки проходят так называемые заявки на обслуживание. Принято говорить, что заявки обслуживаются каналами. Каналы могут быть разными по назначению, характеристикам, они могут сочетаться в разных комбинациях. Если канал свободен, то заявка обслуживается каналом. В случае занятости канала заявки либо становятся в очередь, либо им отказывают в обслуживании и они исключаться из дальнейшего рассмотрения (СМО с отказами). Важно, что заявки, с точки зрения системы, абстрактны: это все то, что желает обслужиться, то есть пройти определенный путь в системе. Каналы являются также абстракцией: это все то, что обслуживает заявки.

Предмет теории массового обслуживания связан с установлением зависимости между характеристиками потока заявок, числом каналов, их производительностью, правилами работы СМО и эффективность обслуживания. Характеристики эффективности СМО обычно следующие:

1) Среднее число обслуживаемых заявок СМО в единицу времени;

2) Среднее число заявок, покидающих СМО не обслуженными;

3) Среднее время ожидания в очереди и т.п.

Случайный характер потока заявок и длительности их обслуживания приводит к тому, что в СМО протекает случайный процесс. Если случайный процесс марковский, то удается описать работу СМО с помощью аппарата обыкновенных дифференциальных уравнений и выразить характеристики обслуживания через параметры СМО и потоки заявок. При изучении СМО обычно выделяют три класса основных задач: задачи анализа поведения систем, статические задачи, операционные задачи.

Обобщенный подход (А схемы)

Основная идея агрегативного подхода предложенного Н.П. Бусленко и положенного в основу обобщенного подхода заключается в том, что рассматриваемая система расчленяется на отдельные подсистемы (агрегаты) таким образом, чтобы каждая из них удовлетворительно описывалась той или иной типовой схемой. Если выделенная подсистема не может быть удовлетворительно описана типовой схемой, то она вновь подвергается очередному разбиению на агрегаты (агрегаты второго уровня) и т.д. Важнейшим моментом здесь является сохранение и отображение связей между выделенными подсистемами. Таким образом, с формальной точки зрения агрегативная модель есть знакомая нам пара

,

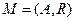где 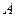- множество математических моделей частей системы (агрегатов);

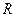- множество операторов, описывающих связи между агрегатами.

По существу, А-схема есть многоуровневая связанная математическая конструкция, компоненты которой могут описываться самыми различными моделям, и основную проблемы составляет искусство согласования достаточно адекватного взаимодействия агрегатов, обеспечивающего нужное подобие объекту моделирования соответствующей машинной реализации этой комплексной модели. Иногда полученная комплексная модель допускает аналитические исследования, в более сложных случаях она выступает, как основа для имитационной модели. По-существу агрегативные модели есть одна из попыток модельного отображения системного характера объектов.

Отдельным важным этапом моделирования является контроль правильности математической модели. Несомненно, что качество математической модели можно оценить только по результатам проведения ней экспериментов. Вместе с тем после построения математической модели целесообразно выполнить следующие действия [80]:

контроль размерностей, включающий правило, согласно которому приравниваться, складываться, перемножаться и делиться могут только величины одинаковой размерности. При переходе к вычислениям добавляется дополнительное требование соблюдения одной и той же системы единиц для значений всех параметров;

проверка порядков, состоящая в сравнении порядков складываемых или вычитаемых величин и исключении из математических соотношений малозначимых параметров;

контроль характера зависимости, предполагающий, что направление и скорость изменения выходных параметров модели должны соответствовать физическому смыслу изучаемых процессов;

· проверка экстремальных ситуаций, которая заключается в наблюдении за выходными результатами модели при приближении значений ее параметров к предельно допустимым. Зачастую это делает математические соотношения более простыми и наглядными (например, при равенстве нулю какой-либо величины);

· контроль физического смысла, связанный с установлением физического смысла результата и проверкой его неизменности при варьировании параметров модели от исходных до промежуточных и граничных значений;

· проверка математической замкнутости, состоящая в выявлении принципиальной возможности решения системы математических соотношений и получении на ее основе однозначно интерпретируемого результата.