2015-02-27
1081
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения.
Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.
Момент импульса замкнутой системы сохраняется.
Момент импульса в классической механике
Связь между силой F, моментом силы τ, импульсом 
и моментом импульса 
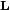
Определение[править | править исходный текст]
Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
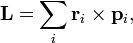
где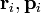 
— радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
(В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообщераспределенной системы это может быть записано как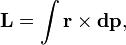 
где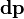 
— импульс бесконечно малого точечного элемента системы).
В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.
Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:
.
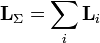Замечание: в принципе момент импульса может быть вычислен относительно любого начала отсчета (получившиеся при этом разные значения связаны очевидным образом); однако чаще всего (для удобства и определенности) его вычисляют относительно центра масс или закрепленной точки вращения твердого тела итп).
Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этиммомент импульса замкнутой системы в любой системе координат не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
В упрощённом виде: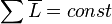 
, если система находится в равновесии.
