Под сложением колебаний понимают нахождение закона результирующих колебаний системы в тех случаях, когда эта система одновременно участвует в нескольких колебательных процессах.
При сложении двух гармонических колебаний одинакового направления и частоты, результирующее смещение будет суммой (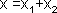 ) смещений
) смещений 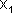 и
и 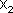 , которые запишутся следующими выражениями:
, которые запишутся следующими выражениями:
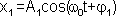 ,
, 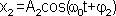 ,
,
Сумма двух гармонических колебаний также будет гармоническим колебанием той же круговой частоты:
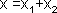 =
= 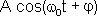 .
.
Значения амплитуды А и начальной фазы φ этого гармонического колебания будет зависеть от амплитуд исходных колебаний и их начальных фаз Если частоты колебаний 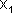 и
и 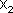 , неодинаковы, векторы А 1 и А 2 будут вращаться с различной скоростью. В этом случае результирующий вектор А пульсирует по величине и вращается с не постоянной скоростью. Результирующим движение уже будет не гармоническое колебание, а сложный колебательный процесс.
, неодинаковы, векторы А 1 и А 2 будут вращаться с различной скоростью. В этом случае результирующий вектор А пульсирует по величине и вращается с не постоянной скоростью. Результирующим движение уже будет не гармоническое колебание, а сложный колебательный процесс.
Биения Биения возникают при сложении колебаний, отличающихся по частоте на небольшую величину, и проявляются в появлении более низкочастотных изменений амплитуды суммарного сигнала, по сравнению с исходными частотами. Амплитуда колебаний при этом меняется от минимального значения равного разности исходных амплитуд до максимального значения, равного сумме амплитуд исходных колебаний, и вновь до минимального значения. Периодом биений является время повторения этого процесса
Величина 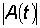 , характеризующая размах колебаний при биениях, изменяется в пределах от
, характеризующая размах колебаний при биениях, изменяется в пределах от 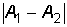 до
до 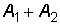 с циклической частотой
с циклической частотой 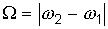 , называемой циклической частотой биений. Поскольку частота биений во много раз меньше частоты колебаний (
, называемой циклической частотой биений. Поскольку частота биений во много раз меньше частоты колебаний (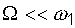 ), то переменную величину
), то переменную величину 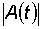 условно называют амплитудой биений. Период биений
условно называют амплитудой биений. Период биений 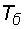 и частота биений
и частота биений 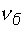 равны:
равны:
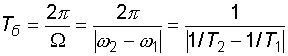 (9.13)
(9.13)
и
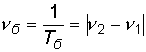 , (9.14)
, (9.14)
где 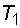 ,
, 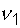 и
и 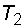 ,
, 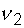 – периоды и частоты складываемых колебаний. Характер зависимости
– периоды и частоты складываемых колебаний. Характер зависимости 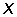 от времени при биениях показан на рис. 9.2 (для случая
от времени при биениях показан на рис. 9.2 (для случая 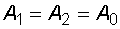 ).
).
 2015-02-27
2015-02-27 8137
8137








