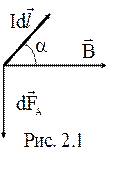Действие магнитного поля на токи, магнитные моменты

На проводники с током, находящиеся в магнитном поле, действуют силы, называемые силами Ампера. Сила Ампера, приложенная к маломуэлементу проводника с током I (рис. 2.1), равна арифметической сумме сил Лоренца, которые действуют на движущиеся в проводнике носители заряда.

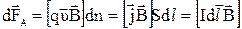, dF_A=Id l Bsina, (2.1)

где dn - количество носителей заряда в элементе проводника длиной d l и сечением S, 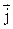- плотность тока в проводнике, I - сила тока в проводнике, 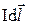- линейный элемент тока, α - угол между векторам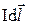и и .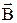

Сила Ампера, действующая в магнитном поле на проводник конеч­ной длины,

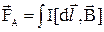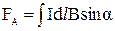, . (2.2)

В частности, если поле однородно, а проводник прямолинейный, то

F = IB l sina. (2.3)

Расчет силы Ампера, действующей на участок длиной l бесконечно длинного проводника с током I₂ со стороны длинного прямолинейного проводника с током I₁, расположенного параллельно данному проводнику, дает величину:

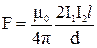, (2.4)

где d - расстояние между проводниками, m_о=4 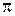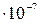Гн/м - магнитная постоянная.

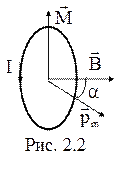На малый замкнутый контур с током (магнитный момент) в однородном магнитном поле действует вращающий момент сил 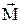(рис. 2.2)

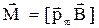, М = р_mВsina, (2.5)

где 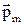- магнитный момент контура с током, а a - угол между векторами магнитного момента и магнитной индукции.

Момент сил стремится установить магнитный момент по направлению магнитной индукции 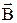в положение устойчивого равновесия. Если внешние силы увеличивают угол a, то они совершают работу против сил магнитного поля и тем самым увеличивают энергию контура, которую можно вычислить следующим способом

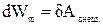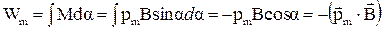, . (2.6)

В неоднородном магнитном поле на магнитный момент дополнительно действует отличная от нуля сила, сообщающая ему поступательное движение

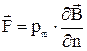, (2.7)

где 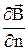- производная вектора магнитной индукции по направлению магнитного момента.