Рассмотрим еще одну линейную операцию над векторами – умножение вектора на число. Результатом этой операции является произведение вектора на число.
Произведением вектора 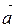 на действительное число a называется вектор
на действительное число a называется вектор 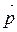 , обозначаемый через
, обозначаемый через 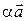 и удовлетворяющий двум условиям:
и удовлетворяющий двум условиям:
1) его длина 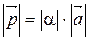 ;
;
2) если a 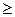 0, то
0, то 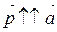 ; если
; если 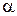 <0, то
<0, то 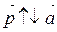 .
.
Алгоритм построения произведения вектора 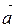 число a таков.
число a таков.
Берем произвольную точку М. Проводим луч 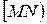 , сонаправленный с вектором
, сонаправленный с вектором 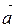 , если a
, если a 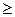 0, и противоположно направленный с вектором
0, и противоположно направленный с вектором 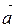 , если
, если 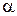 <0. На луче
<0. На луче 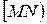 от начала М откладываем отрезок MP, длина которого в
от начала М откладываем отрезок MP, длина которого в 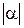 раз больше длины вектора
раз больше длины вектора 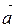 . Вектор
. Вектор 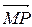 - искомый вектор
- искомый вектор 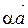 .
.
Продемонстрируем этот алгоритм на конкретном примере. Построим вектор 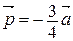 , если
, если 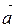 - данный вектор.
- данный вектор.
Возьмем произвольную точку А. Так как 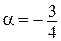 <0, то проводим луч
<0, то проводим луч 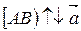 (рис. 7). На луче
(рис. 7). На луче 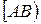 строим такую точку С, что
строим такую точку С, что 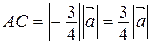 . Тогда
. Тогда 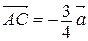 - искомый вектор.
- искомый вектор.
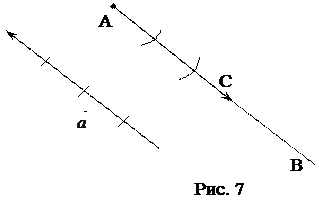 |
 2015-02-27
2015-02-27 346
346








