2015-02-27
1051
В полупроводниках так же, как и в металлах, наблюдаются термоэлектрические явления. Первое термоэлектрическое явление, называемое эффектом Зеебека, заключается в возникновении электродвижущей силы между разомкнутыми концами цепи, состоящей из разнородных проводящих ток материалов, при наличии разности температур их спаев. В простейшем случае, когда цепь состоит из двух разнородных материалов, спаянных концами друг с другом, термоэдс dE, возникающая в такой термопаре, в небольшом температурном интервале примерно пропорциональна разности температур T и T+dT холодного и горячего спаев:
dE = α∙dT, (2.30)
где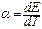 
– коэффициент термоэдс (коэффициент Зеебека). Он численно равен величине термоэдс, возникающей в данной цепи при разности температур спаев dT =1K.
Коэффициент зависит от рода материалов, из которых составлена цепь, от их термической и механической обработки, от состава и концентрации примесей в них, а также от температуры. В полупроводниках наибольшими коэффициентами термоэдс обладают термопары, составленные из материалов разной проводимости, т.е. из полупроводников n-типа и р-типа. На рис. 2.19 представлены термопары, составленные из металлов и полупроводников.
Второе термоэлектрическое явление, называемое эффектом Пельтье, обратно эффекту Зеебека. Оно состоит в том, что при прохождении тока в цепи, состоящей из разнородных материалов, в одном из контактов выделяется сверх джоулевой теплоты дополнительная теплота (тепло Пельтье), во втором же контакте эта теплота поглощается.
В результате температуры контактов оказываются различными. При изменении направления тока на обратное знак эффекта в обоих контактах изменяется. На рис. 2.20 представлены термоэлементы из металлов и полупроводников.
|
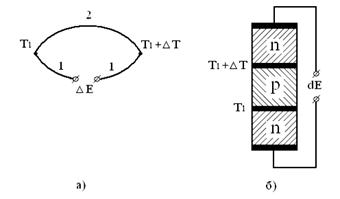
Рис. 2.19. Схемы термопар
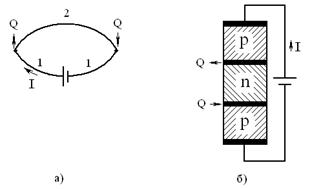
Рис. 2.20. Схемы термоэлементов
Количество выделенной или поглощенной в контактах теплоты Пельтье пропорционально прошедшему через контакты количеств электричества, т.е. силе тока I в цепи и времени его прохождения t:
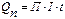, (2.31)
где П – коэффициент Пельтье, численно равный количеству теплоты Пельтье, выделенной или поглощенной в контакте при прохождении через него единицы количества электричества.
Третье термоэлектрическое явление, называемое эффектом Томсона, представлено на рис. 2.21 и заключается в том, что при наличии градиента температуры вдоль однородного проводящего материала, по которому проходит ток I, в элементе длины dx в зависимости от направления тока по отношению к направлению градиента температуры выделяется или поглощается сверх джоулевой теплоты дополнительное количество теплоты, пропорциональное градиенту температуры, величине тока, времени его прохождения и длине элемента:
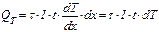, (2.32)
где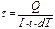 
– коэффициент Томсона, зависящий от природы материала, по которому проходит электрический ток и от температуры.
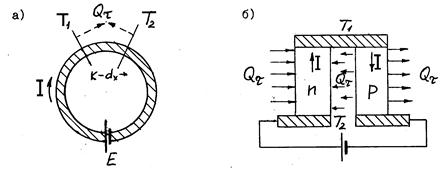
Рис. 2.21. Эффект Томсона: а – в металлическом кольце; б – в полупроводниковом термоэлементе
С приближением температуры к абсолютному нулю τ также стремится к нулю.
Между всеми тремя термоэлектрическими коэффициентами имеется тесная связь, которая была впервые получена математически Томсоном и называется соотношениями Кельвина (Томсона):
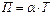; (2.33)
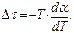(2.34)
Все три величины α (Т), П (Т) и D τ = τ 1- τ 2 связаны между собой простыми соотношениями. Это позволяет вычислять их значение для любого материала, если известна хотя бы одна из этих величин. Наиболее удобной для измерения является α (Т) благодаря сравнительной простоте определения ее температурной зависимости.
В настоящей работе значение коэффициента термоэдс используется для вычисления потенциала Ферми в полупроводниках. Для этого получим необходимую формулу, связывающую потенциал Ферми с коэффициентом Зеебека.
Предварительно вспомним понятие об уровне Ферми. В металлах уровнем Ферми считается такой энергетический уровень, ниже которого при абсолютном нуле все состояния заполнены электронами, а все более высокие энергетические состояния свободны. При конечной температуре Т состояния около уровня Ферми в пределах интервала энергии 2 кТ частично заполнены. Вероятность нахождения электрона в любом данном состоянии связана с разностью энергии между этим состоянием и уровнем Ферми.
Также можно считать, что в полупроводниках вероятность нахождения электрона в любом данном состоянии зависит от его энергии. Разность между энергией электрона и уровнем Ферми связана с этой вероятностью математически так же, как и в металле. Воспользовавшись представлениями электронной теории, можно дать краткое качественное объяснение всем термоэлектрическим явлениям. Мы рассмотрим причины возникновения термоэдс в цепи, состоящей из спаянных своими концами двух разнородных материалов, проводящих электрический ток.
Пусть работы выхода электронов из этих тел равны:
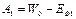; (2.35)
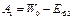, (2.36)
где W 0 – энергия покоящегося электрона, находящегося вне тела;
ЕФ 1 и ЕФ 2 – уровни Ферми в первом и втором телах соответственно.
При осуществлении контакта между такими двумя телами возникает контактная разность потенциалов:
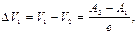(2.37)
где e – заряд электрона; A 1 и А 2 – работа выхода. Если спаять и вторые концы, то скачок потенциала в области второго спая
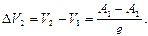(2.38)
При одинаковой температуре спаев результирующая разность потенциалов, равная алгебраической сумме скачков потенциалов, нулевая, т.к. работы выхода одинаковы.
Если температуры спаев различны, то результирующая разность потенциалов не будет равна нулю, а проявится как контактная термоэдс. Это происходит оттого, что положение уровня Ферми в теле, определяющее величину работы выхода, зависит от температуры. Кроме контактной термоэдс, существует еще объемная термоэдс, которая возникает вследствие диффузии электронов проводимости от более нагретого участка с большей концентрацией их к менее нагретому с меньшей концентрацией. После установления динамического равновесия на концах тела устанавливается разность потенциалов, проявляющаяся как термоэдс. В полупроводниках диффундировать могут не только электроны, но и дырки, при этом холодный конец приобретает положительный заряд, а более горячий – отрицательный. Поскольку в полупроводниках электроны проводимости или дырки представляют собой невырожденный газ, а энергия теплового движения и их концентрация сильно зависят от температуры, то положение уровня Ферми, и, следовательно, работы выхода электронов в полупроводниках также зависят от температуры. Поэтому в полупроводниках отлична от нуля и значительна по величине объемная термоэдс. Она может быть больше контактной термоэдс. В термопаре, состоящей из полупроводников разной проводимости, объемные составляющие термоэдс каждой ветви складываются. Поэтому она и обладает наибольшей термоэдс, но мы за неимением таких термопар будем пользоваться парой металл-полупроводник или определять только объемную составляющую полупроводникового материала.
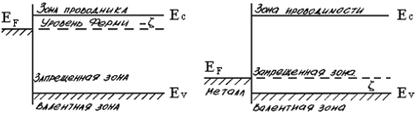
На рис. 2.22 приведена схема энергетических уровней контакта полупроводника с металлом при равновесии.
а) б)
Рис. 2.22. Схема контакта полупроводника с металлом при равновесии (уровень Ферми непрерывен): а – n-полупроводник; б – p-полупроводник.
Рассмотрим подробнее случай контакта полупроводника n-типа с металлом, но точно те же соображения применимы для полупроводника р-типа. Предположим, что электрон переходит из металла в полупроводник n-типа. Переход электрона в зону проводимости полупроводника связан с поглощением некоторого количества потенциальной энергии – ζ. Здесь ζ – это потенциал Ферми. Он отрицателен, если носитель переходит в область с большей энергией. Если поменять направление движения носителя, то знак потенциала Ферми изменится, в этом случае электрон теряет избыточную энергию. Найдем формулу для коэффициента ТЭДС. Выше было показано, что термоэдс, возникающая в термопаре, состоит из двух частей – контактной и объемной. Математически это можно записать так:
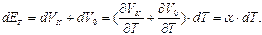(2.39)
Откуда видно, что
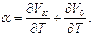(2.40)
Определим обе составляющие коэффициента термоэдс. При расчетах объемную термоэдс в металле не будем учитывать вследствие ее малости. Кроме того, поскольку положение уровня Ферми в металле практически не зависит от температуры, то контактная составляющая термоэдс будет определяться в основном лишь температурной зависимостью уровня Ферми в полупроводнике.
Контактная разность потенциалов между металлом и полупроводником:
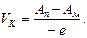(2.41)
Работа выхода из полупроводника может быть записана так:
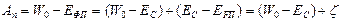, (2.42)
где ЕС – уровень нижней границы зоны проводимости в полупроводнике. Здесь первая скобка от температуры не зависит, а вторая зависит, поскольку с изменением температуры изменяется уровень Ферми в полупроводнике. Поэтому контактная часть термо-эдс dVK, равная сумме контактных скачков потенциалов в обоих спаях термопары, выражается так:
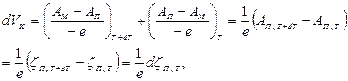(2.43)
где ζ – потенциал Ферми в полупроводнике (при равновесии индекс можно не писать).
Тогда
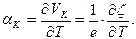(2.44)
Поскольку из электронной теории
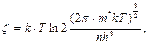(2.45)
где m * – эффективная масса электрона;
k – постоянная Больцмана;
h – постоянная Планка;
n – концентрация носителей тока,
то
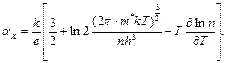(2.46)
Теперь вычислим объемную часть термоэдс. При диффузии давление электронного газа, подчиняющегося классической статистике Максвелла, как и давление обычного молекулярного газа:
P = nkT, (2.47)
т.е. монотонно зависит от концентрации носителей тока и от температуры. Если внутри полупроводника выделить объем в виде прямого цилиндра (рис. 2.23) с образующей dx, параллельной направлению градиента температуры, и с основаниями единичной площади, то давление электронного газа на его основание будет различным: если в сечении с координатой x при температуре Т оно равно Р, то в точках второго основания с координатой x+dx при температуре Т+dt оно будет равно P1=P+dP.
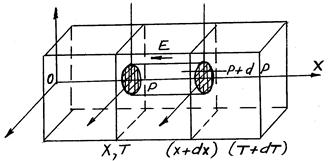
Рис. 2.23. Полупроводник с током
Наряду с возникновением градиента давления электронного газа в полупроводнике при диффузии электронов создается электрическое поле, препятствующее дальнейшей диффузии электронов. В состоянии динамического равновесия разность давлений уравновешивается силой электрического поля, действующего на электроны проводимости, содержащиеся внутри данного объема. Это можно записать так:
dP =- en dx. (2.48)
Следовательно, напряженность электрического поля, вызванного диффузией носителей тока в полупроводнике при равновесии, запишется так:
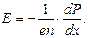(2.49)
Но, поскольку напряженность есть градиент потенциала с обратным знаком, то
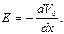(2.50)
Сравнивая эти равенства, видим, что
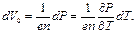(2.51)
Следовательно,
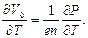(2.52)
Подставив в это выражение значение давления из формулы (2.47),найдем:
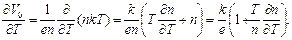(2.53)
Таким образом, коэффициент объемной термоэдс
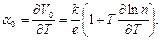(2.54)
Тогда полный коэффициент термоэдс
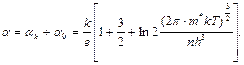(2.55)
Подставив сюда вместо последнего слагаемого его значение из формулы (2.44), выразим коэффициент термоэдс через потенциал Ферми:
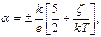(2.56)
где знак "плюс" относится к полупроводнику р-типа, а знак "минус" к полупроводнику n-типа. Из этой формулы легко находится выражение для потенциала Ферми. Это и будет расчетная формула:
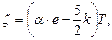(2.57)
где Т – температура, при которой производился замер коэффициента термоэдс.
