2015-02-27
1713
Рассмотрим автономную систему
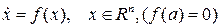(4.1)
и будем исследовать устойчивость ее положения равновесия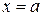 
.
Определение 4.1. Положение равновесия 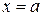системы (4.1) называется устойчивым по Ляпунову, если для любого 
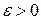можно указать 
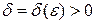такое, что:
1) если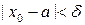 
, то решение 
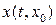системы (4.1) определено при всех 
;
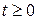2) при всех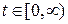 
выполнено условие 
.
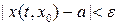Если к тому же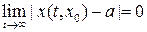 
, то состояние равновесия 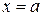асимптотически устойчиво по Ляпунову.
Пусть V (x) – функция переменной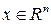 
. Будем говорить, что функция V (x) положительно определена в окрестности U точки 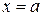, если 
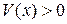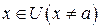при 
и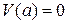 
. Если же в окрестности U выполнены условия 
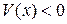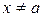при 
и 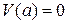, то будем говорить, что функция V(x) отрицательно определена в окрестности U.
Приведенная ниже теорема А.М.Ляпунова является одной из центральных теорем так называемого второго метода Ляпунова, играющего важную роль в качественной теории дифференциальных уравнений.
Теорема 4.1. (Терема Ляпунова об устойчивости ).Если в некоторой окрестностиUположения равновесия 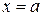системы (4.1) существует непрерывно дифференцируемая положительно определенная функция V(x) такая, что ее производная в силу этой системы 
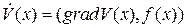не положительна в указанной окрестности, то положение равновесия устойчиво по Ляпунову.
Теорема 4.2. (Теорема Ляпунова об асимптотической устойчивости). Пусть в некоторой окрестности U положения равновесия 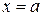системы (4.1) существует непрерывно дифференцируемая положительно определенная функция V(x) такая, что ее производная 
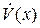в силу этой системы отрицательно определена в U. Тогда положение равновесия 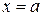асимптотически устойчиво по Ляпунову.
Везде ниже, без ограничения общности, будем считать, что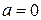 
, т.е. 
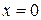– положение равновесия системы (4.1), и будем исследовать устойчивость этого положения равновесия.
Теорема 4.2 не дает оценки скорости стремления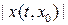 
к нулю при 
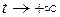. Следующее утверждение позволяет получить такую оценку.
Теорема 4.3. Пусть 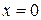положение равновесия системы (4.1) и существует положительно определенная в некоторой окрестности точки 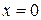функция V(x) такая, что
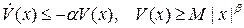, (4.2)
где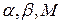 
– некоторые положительные числа.
Тогда существует такая постоянная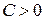 
, что 
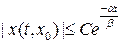при 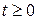для всех достаточно малых 
.
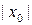Существуют теоремы, устанавливающие условия неустойчивости положения равновесия системы (4.1). Наиболее сильной из них является теорема Четаева. Для того, чтобы сформулировать эту теорему, введем некоторые дополнительные понятия. Пусть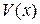 
– непрерывно дифференцируемая функция, определенная в области 
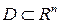, содержащей начало координат 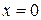. Предположим, что 
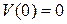и что существует сколь угодно близкая к началу координат точка 
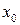такая, что 
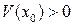. Выберем 
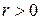так, чтобы шар 
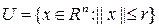содержался в 
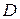и положим
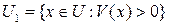. (4.3)
Множество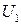 
непустое и содержится в 
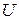(рис.4.1). Его границу составляют поверхность 
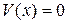и сфера 
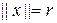. Поскольку 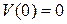, начало координат лежит на границе множества .
|
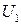Теорема 4.4. (теорема Четаева). Пусть 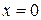– положение равновесия системы (4.1). Пусть 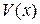– непрерывно дифференцируемая функция такая, что 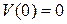и 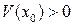для некоторой точки 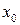такой, что 
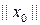произвольно малая величина. Определим 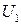соотношением (4.3) и предположим, что 
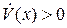в 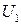. Тогда 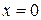– неустойчивое положение равновесия системы (4.1).
Приведем несколько примеров, иллюстрирующих применение теорем Ляпунова и Четаева.
Пример 4.1. Пусть уравнения возмущенного движения имеют вид
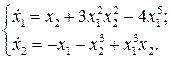
Здесь, очевидно,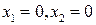 
– положение равновесия. Для исследования его на устойчивость рассмотрим функцию 
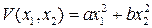. Производная этой функции в силу рассматриваемой системы
.
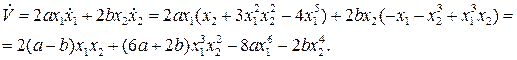Положим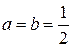 
. Тогд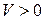а 
, а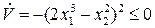 
Следовательно, возмущенное движение устойчиво по Ляпунову. Однако асимптотическую устойчивость мы гарантировать не можем.
Пример 4.2. Рассмотрим систему
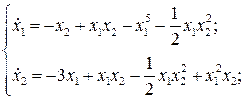
В качестве функции Ляпунова возьмем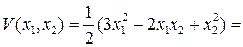 
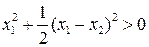. Имеем,
.
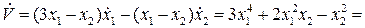
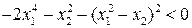По теореме 4.2 состояние равновесия (0,0) асимптотически устойчиво по Ляпунову.
Пример 4.3. Рассмотрим систему
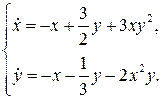
Будем искать функцию Ляпунова в виде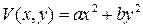 
. Тогда 
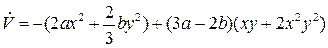. Полагая 
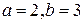, получим 
.
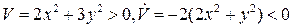Заметим, что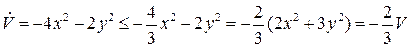 
. Кроме того, 
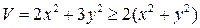. То есть, выполнены соотношения (4.2) с 
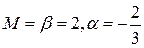. Поэтому, согласно теореме 4.3, существует такая постоянная 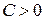, что 
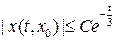при 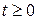для всех достаточно малых .
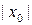Пример 4.4.. Рассмотрим систему
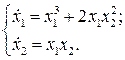
Пусть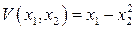 
. 
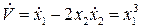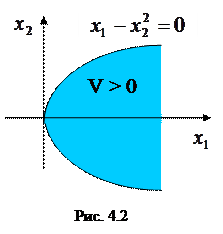
. Очевидно, 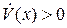в той области на плоскости 
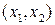, где 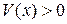(рис. 4.2). Значит, выполнены все условия теоремы Четаева, и состояние равновесия 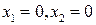неустойчиво по Ляпунову.
