Пусть корень уравнения f(x)=0 отделен на отрезке [a, b]. Причем производные f ‘(x) и f ’’(x) непрерывны и сохраняют постоянные знаки.
Геометрический смысл метода касательных состоит в том, что дуга кривой y=f(x) заменяется касательной к этой кривой.
Рассмотрим случай, когда f ‘(x) f ’’(x)>0, т.е. f ‘(x) и f ’’(x) имеют одинаковые знаки (рис. 2.11)

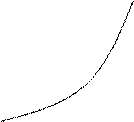


Рис. 2.11
Проведем касательную к кривой y=f(x) в точке B0(b, f(b)).
Уравнение касательной в точке B0: y-f(b)=f ’(b)(x-b).
Полагая y=0, найдем 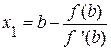 .
.
Теперь 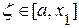 .
.
Применяя метод еще раз для отрезка 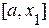 , получим
, получим 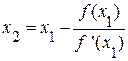 .
.
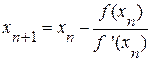 (2.4)
(2.4)
Пусть теперь f ‘(x) f ’’(x)<0 (рис. 2.12)
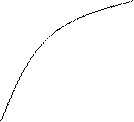
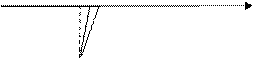

Рис. 2.12
Если снова провести касательную к кривой в точке B, то она пересечет ось ox в точке не принадлежащей отрезку [a, b].
Поэтому проведем касательную в точке A0(a, f(a)).
Ее уравнение y-f(a)=f ‘(a)(x-a).
Находим x1, полагая y=0
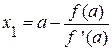 .
.
Корень 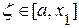 , применяя снова метод касательных, получим
, применяя снова метод касательных, получим
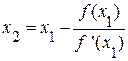 и т.д., тогда
и т.д., тогда
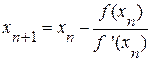 (2.5)
(2.5)
Сравнивая формулы (2.4) и (2.5) между собою, замечаем, что они отличаются друг от друга только выбором начального приближения: в первом случае за x0 принимают конец b отрезка, во втором – конец a. При выборе начального приближения корня необходимо руководствоваться правилом: за начальную точку следует выбрать тот конец отрезка [a, b], в котором знак функции совпадает со знаком производной.
Условие окончания вычислительного процесса: 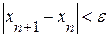 , где
, где 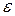 - заданная точность.
- заданная точность.




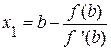 .
.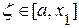 .
.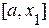 , получим
, получим 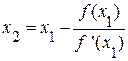 .
.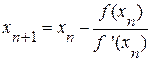 (2.4)
(2.4)
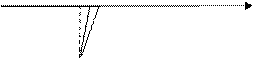

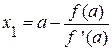 .
.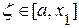 , применяя снова метод касательных, получим
, применяя снова метод касательных, получим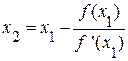 и т.д., тогда
и т.д., тогда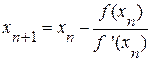 (2.5)
(2.5)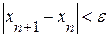 , где
, где 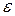 - заданная точность.
- заданная точность. 2015-02-04
2015-02-04 556
556








