Методы хорд и касательных дают приближения корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом, тогда уточнение корня происходит быстрее.
Пусть дано уравнение f(x)=0, корень отделен на отрезке [a, b].
Рассмотрим случай, когда f ‘(x) f ’’(x)>0 (рис. 2.13)

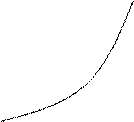
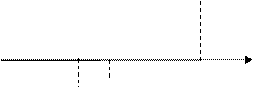

Рис. 2.13
В этом случае метод хорд дает приближенное значение корня с недостатком (конец b неподвижен), а метод касательных – с избытком (за начальное приближение берем точку b).
Тогда вычисления следует проводить по формулам:
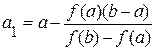 ;
; 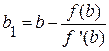 .
.
Теперь корень ξ заключен в интервале [a1, b1].
Применяя к этому отрезку комбинированный метод, получим:
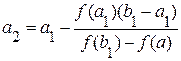 ;
; 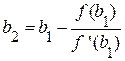 и т.д.
и т.д.
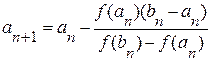 ;
; 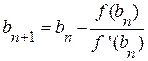 (2.6)
(2.6)
Если же f ‘(x) f ’’(x)<0 (рис. 2.14), то рассуждая аналогично, получим следующие формулы для уточнения корня уравнения:


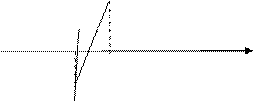

Рис. 2.14
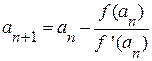 ;
; 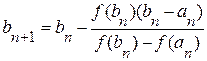 .
.
Вычислительный процесс прекращается, как только 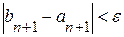 .
.
Задания. Найти наименьший положительный корень уравнения одним из методов, указанных преподавателем.
1. 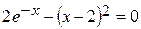 | 2. 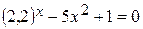 |
3. 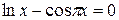 | 4. 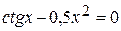 |
5. 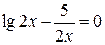 | 6. 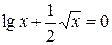 |
7. 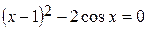 | 8. 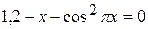 |
9. 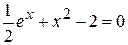 | 10. 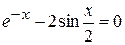 |
11. 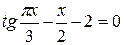 | 12. 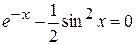 |
13. 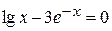 | 14. 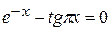 |
15. 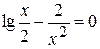 | 16. 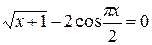 |
17. 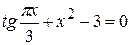 | 18. 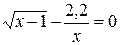 |
19. 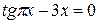 | 20. 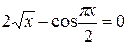 |
21. 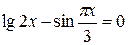 | 22. 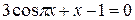 |
23. 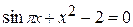 | 24. 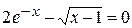 |
25. 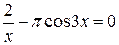 | 26. 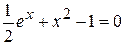 |
3. АППРОКСИМАЦИЯ ФУНКЦИЙ
Будем считать, что некоторый процесс характеризуется двумя изменяющимися величинами x и y, из которых x выбирается как независимая, а y – как зависимая переменная величина. Предположим, сто каждому значению переменной x соответствует единственное значение переменной y, т.е. y является функцией x.
На практике часто известна аналитическая зависимость между x и y, т.е. функцию нельзя записать в виде y=f(x). В некоторых случаях эта зависимость известна, но вычисления значений функций громоздко. В этих случаях прибегают к табличному способу задания функций. Таблица представляет собой набор значений функций для последующих значений аргументов:
| x | x0 x1 …. xn |
| y | y0 y1 …. yn |
Эти значения либо вычислены, либо получены экспериментально.
Преимуществом табличного способа задания функций является то, что для каждого значения аргумента, содержащегося в таблице, без вычислений можно найти значение функции.
Недостаток этого способа в том, что нельзя составить таблицу для всех значений аргумента, всегда найдутся такие значения аргумента, которых нет в таблице.
Таким образом, возникает задача о приближении (аппроксимации) функции: данную функцию y=f(x) требуется приближенно заменить (аппроксимировать) некоторой функцией y(x) так, чтобы отклонения (в некотором смысле) Y(x) от f(x) в заданной области было наименьшим. Функция Y(x) называется аппроксимирующей.






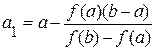 ;
; 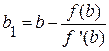 .
.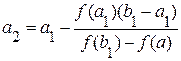 ;
; 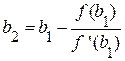 и т.д.
и т.д.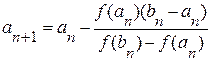 ;
; 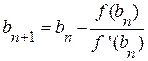 (2.6)
(2.6)
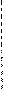



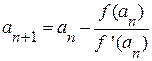 ;
; 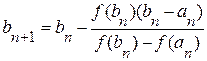 .
.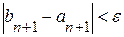 .
.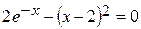
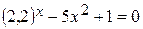
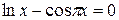
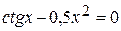
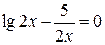
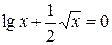
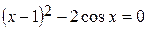
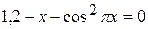
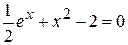
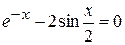
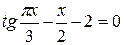
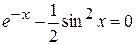
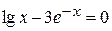
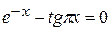
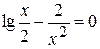
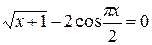
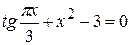
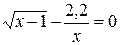
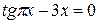
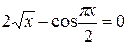
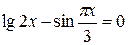
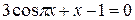
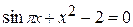
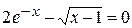
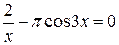
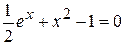
 2015-02-04
2015-02-04 1337
1337
