Пусть функция задана таблично
| x0 | x1 | … | xn |
| y0 | y1 | … | yn |
Построим многочлен Ln(x), такой, что
Ln(x0)= y0, Ln(x1)= y1, …, Ln(xn)= yn. (3.1)
При такой постановке задачи узлы интерполяции x0, x1, …, xn могут произвольно отстоять друг от друга, т.е. узлы интерполяции неравноотстоящие.
Задача имеет решение, если степень многочлена Ln(x) будет не выше n.
Представим многочлен Ln(x) в виде:
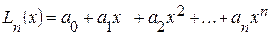 ,
,
где ai (i=0,1,…,n) неизвестные коэффициенты, которые надо найти. Из условий (3.1) следует, что
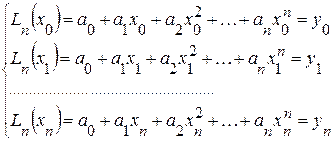
Таким образом, получаем систему из n+1 уравнение для нахождения (n+1) неизвестных a0, a1, …, an
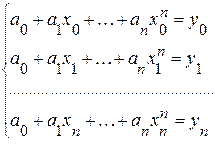 (3.2)
(3.2)
определитель которой
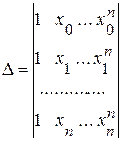 отличен от нуля, если x0, x1, …, xn различны.
отличен от нуля, если x0, x1, …, xn различны.
Тогда существует единственное решение этой системы
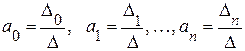 .
.
Найдя коэффициенты a0, a1, …, an, запишем многочлен Ln(x). Однако, каждый раз решать систему уравнений (3.2) затруднительно, поэтому рассмотрим другой способ построения Ln(x). Запишем его в виде:
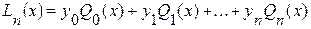 . (3.3)
. (3.3)
Из выражения (4.3) следует, что функция Qn(x) должна удовлетворять условиям:
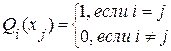 .
.
Легко видеть, что этим условиям отвечает многочлен вида:
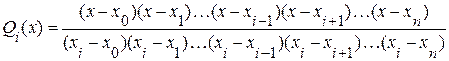 (3.4)
(3.4)
В точках 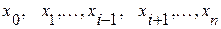 функция Qi(x) обращается в 0, а в точке xi равна 1.
функция Qi(x) обращается в 0, а в точке xi равна 1.
Тогда, подставляя в (3.3) выражение (3.4), окончательно получим:
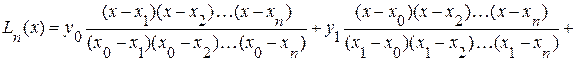
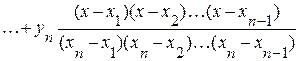 .
.
Этот многочлен называется интерполяционным многочленом Лагранжа.
В сокращенном виде его можно записать так:
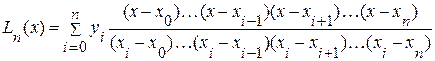 .
.
 2015-02-04
2015-02-04 529
529








