Критерий принятия решения, используемый в этапе 2 описывался формулой (7.7) следующим образом: 
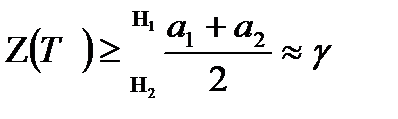
Популярный критерий выбора порога 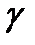 для принятия двоичного решения в выражении (3.7) основан на минимизации вероятности ошибки. Вычисление этого минимального значения ошибки
для принятия двоичного решения в выражении (3.7) основан на минимизации вероятности ошибки. Вычисление этого минимального значения ошибки 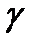 =
= 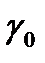 начинается с записи связи отношения плотностей условных вероятностей и отношения априорных вероятностей появления сигнала. Поскольку плотность условной вероятности
начинается с записи связи отношения плотностей условных вероятностей и отношения априорных вероятностей появления сигнала. Поскольку плотность условной вероятности 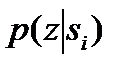 также называется функцией правдоподобия
также называется функцией правдоподобия 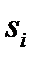 формулировка
формулировка
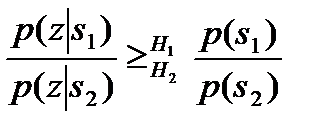 (7.3)
(7.3)
есть критерием отношения функций правдоподобия (см. приложение Б). В этом неравенстве 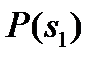 и
и 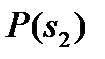 являются априорными вероятностями передачи сигналов
являются априорными вероятностями передачи сигналов 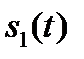 и
и 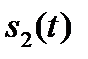 , a
, a 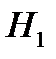 и
и 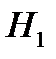 — две возможные гипотезы. Правило минимизации вероятности ошибки (формула (3.3)) гласит, что если отношение функций правдоподобия больше отношения априорных вероятностей, то следует выбирать гипотезу
— две возможные гипотезы. Правило минимизации вероятности ошибки (формула (3.3)) гласит, что если отношение функций правдоподобия больше отношения априорных вероятностей, то следует выбирать гипотезу 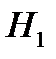 .
.
В разделе Б.3.1 показано, что при 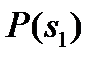 =
= 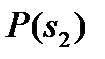 и симметричных функциях правдоподобия
и симметричных функциях правдоподобия 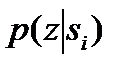 (i=l, 2) подстановка формул (3.5) и (3.6) в формулу (3.3) дает
(i=l, 2) подстановка формул (3.5) и (3.6) в формулу (3.3) дает
(7.4)
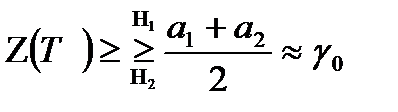
где 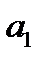 — сигнальный компонент
— сигнальный компонент 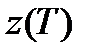 при передаче
при передаче 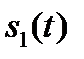 , а
, а 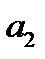 — сигнальный компонент
— сигнальный компонент 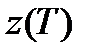 при передаче
при передаче 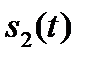 . Порог
. Порог 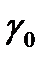 , представленный выражением
, представленный выражением 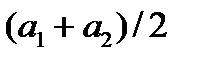 , — это оптимальный порог для минимизации вероятности принятия неверного решения в этом важном частном случае. Описанный подход называется критерием минимальной ошибки.
, — это оптимальный порог для минимизации вероятности принятия неверного решения в этом важном частном случае. Описанный подход называется критерием минимальной ошибки.
Для равновероятных сигналов оптимальный порог 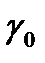 , как показано на рис, 3.2, проходит через пересечение функций правдоподобия. В заключение отметим, что поскольку отношение
, как показано на рис, 3.2, проходит через пересечение функций правдоподобия. В заключение отметим, что поскольку отношение 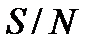 является безразмерным, таким же является и отношение
является безразмерным, таким же является и отношение 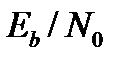 . Для проверки можно вычислить единицы измерения:
. Для проверки можно вычислить единицы измерения:
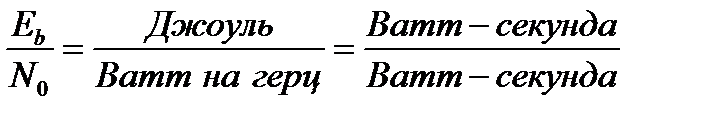 .
.
Основная литература 4[155:174].
Дополнительная литература 13[78:96].
Контрольные вопросы
1.Что такое отношение сигнал\шум?
2. Как детектируется двоичные сигналы в шуме?
3.Что такое критерий минимальной ошибки?
 2015-02-27
2015-02-27 831
831








