Метод использования «ключика»

Задача 1. Решите в целых числах: 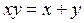. Найти .

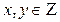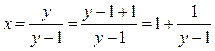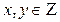Решение. (Решение данной задачи другим способом рассматрива­ется в первой части - задача №5.) , где (1)

Очевидно, что если 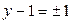, тогда 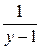- целое число.

1 сл.: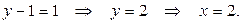

2сл.: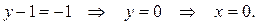

Ответ: 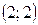и .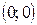

Обобщение: «ключиком» к исходной задаче 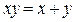является вы­ражение 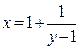. Что же можно варьировать?

Замечание: В числителе дроби 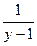можно ставить любое целое число, с помощью которого получаются новые задачи.

Например, возьмем в качестве 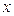выражение 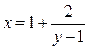, 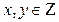и из него получим исходную задачу. Имеем 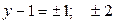. 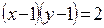, 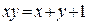. Получили новую задачу:

Задача 2. Решите в целых числах уравнение .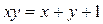

Решение. Так как 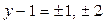, то мы должны рассмотреть че­тыре случая.

1 сл.: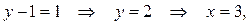

2 сл.: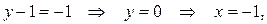

3 сл.: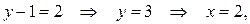

4 сл.: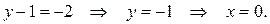

Ответ: .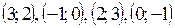

Замечание: 1) В качестве примера рассмотрим случаи 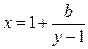, где 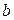- простое число, составное, нечетное.

2) Рассмотрим случа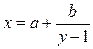й при 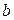- простом, составном, нечетном.

В общем случае: 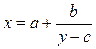. Если 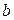- простое число, то .

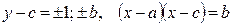До сих пор меняли только 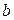, но задачу можно видоизменить меняя значения 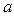и 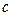. Рассмотрим «ключик» в виде: ; . , .

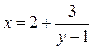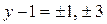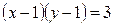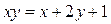Задача 3. Решите в целых числах уравнение .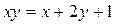

Решение. Если 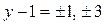, тогда 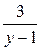- целое число. Рассмот­рим следующие случаи:

1 сл.: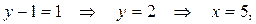

2 сл.: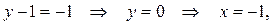

3 сл.: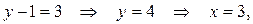

4 сл.: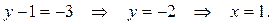

Ответ: .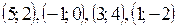

Рассмотрим следующую задачу: , , .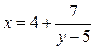

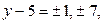
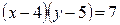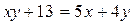Задача 4. Решите в целых числах уравнение .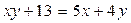

Решение. Если 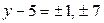, тогда 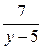- целое число. Реше­нием данной задачи будет:

1 сл.: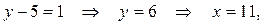

2 сл.: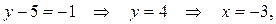

3 сл.: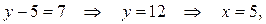

4 сл.: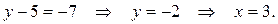

Ответ: .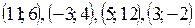

Усложним теперь задачу:

, (*)

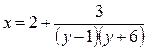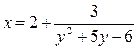Задача 5. Решите в целых числах .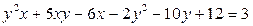

Решение. Разложим левую часть данного уравнения на множители с помощью метода группировки. 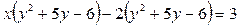, 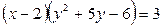. Из (*) очевидно, что если 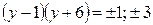, тогда 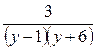- целое число.

1 сл.: 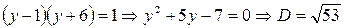- иррациональ­ное число,

2сл.: 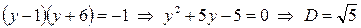- иррацио­нальное число,

3сл.: 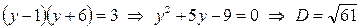- иррацио­нальное число,

4сл.: 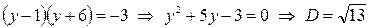- иррацио­нальное число,

Следовательно, 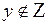а значит, данные уравнения целых решений не имеют.

Ответ: решений в целых числах нет.

Творческое задание: Рассмотреть задачи с «ключиком». Составить авторские задачи по данному методу.