Лекция №1
Решение уравнений в целых и натуральных числах
Задачи на решение уравнений в целых числах довольно часто встречаются в олимпиадных заданиях. Поэтому целесообразно рассмотреть решение задач такого характера. В данной лекции приведены основные методы решения уравнений в целых и натуральных числах и тренировочные упражнения для закрепления каждого из рассмотренных методов.
При решении уравнений степени выше первой можно условно выделить следующие методы решения:
1. Методом разложения на множители.
2. Метод использования «ключика».
3. Решение уравнений с двумя переменными как квадратных относительно какой-либо переменной.
4. Метод остатков.
Метод разложения на множители
При решении методом разложения на множители рекомендуется повторить: формулы сокращенного умножения, способ группировки, метод выделения полного квадрата.
Задача 1. Решите уравнение в целых числах: 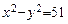
Решение. Разложим левую часть данного уравнения на множители: 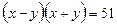 . Так как
. Так как 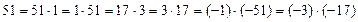 , то решение данного уравнения сводится к решению восьми систем:
, то решение данного уравнения сводится к решению восьми систем:
1) 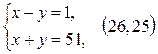 ;
;
2) 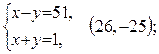
3) 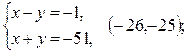
4) 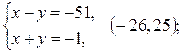
5) 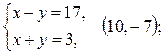
6) 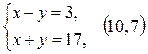
7) 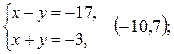
8) 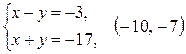 .
.
Ответ: 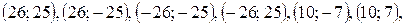
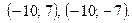
Рассмотрим первую задачу в следующем виде: 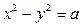 , где
, где 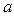 – любое целое число.
– любое целое число.
Пусть 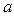 - целое отрицательное число. Например:
- целое отрицательное число. Например: 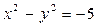 .
.
Задача 2. Решите уравнение в целых числах: 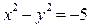
Разложив левую и правую части данного уравнения на множители соответственно: 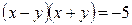 и
и 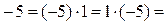
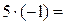
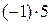 , решим системы:
, решим системы:
1) 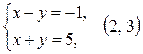 ;
;
2) 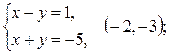
3) 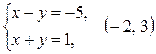 ;
;
4) 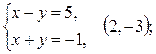
Ответ: 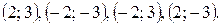
А как же изменится решение, если мы запишем условие задачи следующим образом: 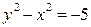 ?
?
В левой части уравнения можно использовать и следующие формулы сокращенного умножения: 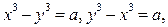
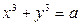 , где
, где 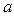 - любое целое число. Например, задача 3.
- любое целое число. Например, задача 3.
Задача 3. Решите в целых числах 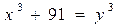 .
.
Решение. Перепишем данное уравнение в следующем виде 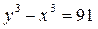 , разложим левую часть на множители
, разложим левую часть на множители 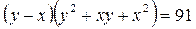 .
.
Заметим, что
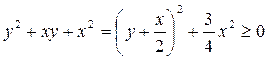
при любом  .
.
Значит, решение данного уравнения сводится к решению следующих систем
1) 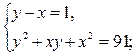
решая данную систему получаем 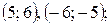
2) 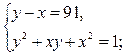
система не имеет решений в целых числах;
3) 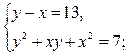
решений в целых числах нет;
4) 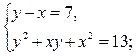
решая данную систему, получаем 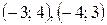 .
.
Проверьте решение данной задачи самостоятельно.
Ответ: 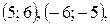
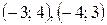 .
.
Теперь усложнить задачу, добавив коэффициенты при 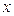 и
и 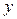 :
: 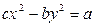 . Например:
. Например:
Задача 4. Решите в целых числах 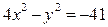 .
.
Разложим левую часть данного уравнения на множители 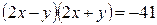 , а так как 41 – простое число, то
, а так как 41 – простое число, то 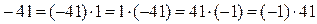 , тогда решим следующие системы:
, тогда решим следующие системы:
1) 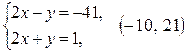 ;
;
2) 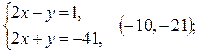
3) 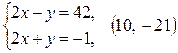 ;
;
4) 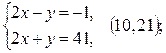
Ответ: 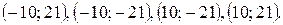
Рассмотрим задачи, в которых требуются некоторые преобразования для сведения к предыдущим случаям.
Задача 5. Решите в целых числах 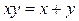 .
.
Решение. Перепишем уравнение в следующем виде 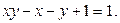
Левую часть данного уравнения разложим на множители, применяя способ группировки. 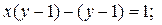
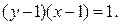
Следовательно,
1) 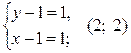 ;
;
2) 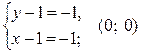 ;
;
Ответ: 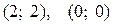 .
.
Задача 6. Решите в целых числах 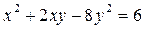 .
.
Решение. Разложим левую часть данного уравнения на множители, для этого перепишем уравнение в следующем виде: 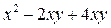
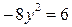 .
.
Применяя способ группировки, получим 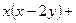
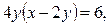
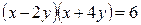 . Так как
. Так как 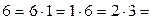
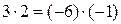
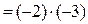 , то получаем следующие случаи:
, то получаем следующие случаи:
1) 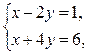
2) 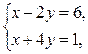
3) 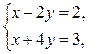
4) 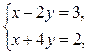
5) 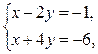
6) 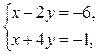
7) 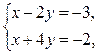
8) 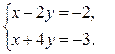
Проверьте решение данной задачи самостоятельно.
Ответ: решений в целых числах нет.
Эту и последующие задачи можно обобщить: 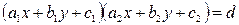 , где
, где 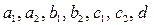 - любые целые числа. Например, пусть
- любые целые числа. Например, пусть 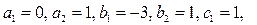
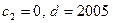 .
.
Можно предложить задачи следующего вида, т.е. в условии задачи изменить слово «целых» на слово «натуральных». При этом перед учениками возникает задача: необходимо вспомнить или повторить - какие же числа относятся к натуральным. Приведем пример.
Задача 7. Решите в натуральных числах 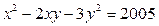 .
.
Решение. Разложим левую часть на множители 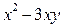
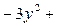
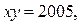
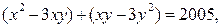
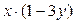
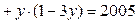 ,
,
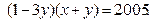
Правая часть раскладывается на множители: 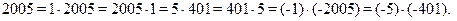 Так как
Так как 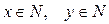 , то
, то 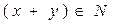 причем
причем 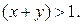 Если
Если 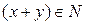 и
и 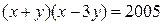 , то
, то 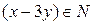 . Тогда решение уравнения сводится к решению следующих систем
. Тогда решение уравнения сводится к решению следующих систем
1) 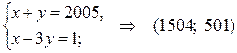 ;
;
2) 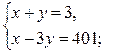
решений в натуральных числах нет,
3) 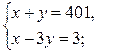
решений в натуральных числах нет.
Ответ: 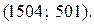
Задача 8. Решите в натуральных числах 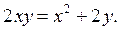
Решение. Перепишем данное уравнение в виде 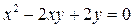 .
.
Данное уравнение также решается методом разложения на множители, однако с помощью формулы разности квадратов или способа группировки мы не сможем разложить на множители левую часть этого уравнения, поэтому целесообразнее использовать метод выделения полного квадрата: 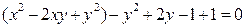 ,
, 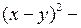
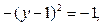
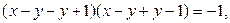
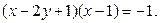
Решение этого уравнения сводится к решению следующих систем:
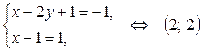
или 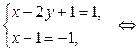 решений в натуральных числах нет.
решений в натуральных числах нет.
Ответ: 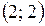 .
.
Рассмотрим более сложные задачи.
Задача 9. Докажите, что уравнение 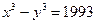 не имеет решений в целых числах.
не имеет решений в целых числах.
Решение. Сначала докажем, что число 1993 простое. Для этого нужно установить, что 1993 не делится на 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 (Убедитесь!). Проверка показывает, что число 1993 простое.
Предположим противное, что существуют целые числа 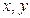 — являющиеся решения уравнения. Тогда из того, что
— являющиеся решения уравнения. Тогда из того, что 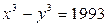 следует, то
следует, то 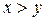 .
.
Запишем данное уравнение в виде 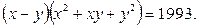
Заметим, что 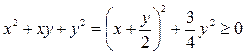 при
при 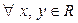 .
.
В силу сделанного выше предположения числа 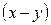 и
и 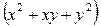 являются целыми положительными и являются делителями простого числа 1993, а это возможно только в двух случаях:
являются целыми положительными и являются делителями простого числа 1993, а это возможно только в двух случаях:
1) 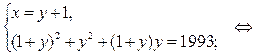
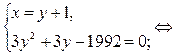
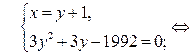
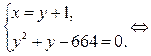
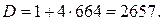
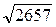 — иррациональное число; следовательно,
— иррациональное число; следовательно, 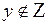 а значит, данная система уравнений целых решений не имеет;
а значит, данная система уравнений целых решений не имеет;
2) 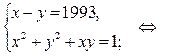
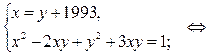
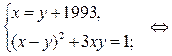
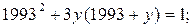 (*)
(*)
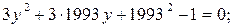
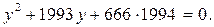
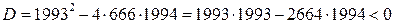
Действительных корней уравнение (*) не имеет, а значит, данная система решений не имеет.
Ответ: данное уравнение не имеет решений в целых числах.
Творческое задание: Составить авторские задачи по данному методу.
 2015-02-27
2015-02-27 2904
2904