Пусть 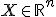 - множество объектов;
- множество объектов; 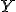 - множество допустимых ответов. Задана обучающая выборка
- множество допустимых ответов. Задана обучающая выборка 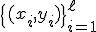 . Задано множество объектов
. Задано множество объектов 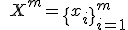 .
.
Требуется найти множество ответов 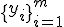 для объектов
для объектов 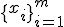 .
.
Алгоритм 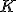 взвешенных ближайших соседей
взвешенных ближайших соседей
На множестве объектов задается евклидова функция расстояния 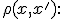
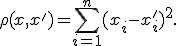
Для произвольного объекта 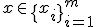 расположим объекты обучающей выборки
расположим объекты обучающей выборки 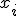 в порядке возрастания расстояний до
в порядке возрастания расстояний до 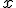 :
:
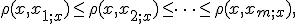
где через 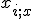 обозначается тот объект обучающей выборки, который является
обозначается тот объект обучающей выборки, который является 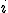 -м соседом объекта
-м соседом объекта 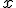 . Аналогичное обозначение введём и для ответа на
. Аналогичное обозначение введём и для ответа на 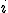 -м соседе:
-м соседе: 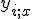 .
.
Таким образом, произвольный объект 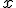 порождает свою перенумерацию выборки. В наиболее общем виде алгоритм ближайших соседей есть
порождает свою перенумерацию выборки. В наиболее общем виде алгоритм ближайших соседей есть
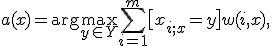
где 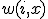 — заданная весовая функция, которая оценивает степень важности
— заданная весовая функция, которая оценивает степень важности 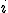 -го соседа для классификации объекта
-го соседа для классификации объекта 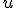 . Так, при
. Так, при 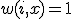 при
при 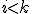 алгоритм соответствует медоду
алгоритм соответствует медоду 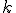 ближайших соседей. Но в задаче с несколькими возможными ответами максимальная сумма голосов может достигаться на нескольких классах одновременно. Неоднозначность можно устранить, если в качестве весовой функции взять нелинейную последовательность, например геометрическую прогрессию: в рассматриваемом примере
ближайших соседей. Но в задаче с несколькими возможными ответами максимальная сумма голосов может достигаться на нескольких классах одновременно. Неоднозначность можно устранить, если в качестве весовой функции взять нелинейную последовательность, например геометрическую прогрессию: в рассматриваемом примере 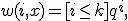 что соответствует методу
что соответствует методу 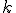 экспоненциально взвешенных ближайших соседей, причем предполагается
экспоненциально взвешенных ближайших соседей, причем предполагается 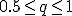 .
.
 2015-02-27
2015-02-27 515
515








