2015-02-27
291
Для временного ряда рассмотрим критерий «восходящих и нисходящих» серий.
| t | |||||||
| 2.8 | 2.3 | 1.5 | 1.3 | 1.2 | 1.1 | 1.0 |
1. Для исследемого временного ряда определяется последовательность знаков, исходя из условий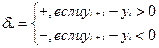 
При этом, если последующее наблюдение равно предыдущему, то учитывается только одно наблюдение.
2. Подсчитывается число серий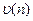 
. Под серией понимается последовательность подряд расположенных плюсов и минусов, причем один плюс или один минус считается серией.
3. Определяется продолжительность самой длинной серии lmak (n)
4. По таблице, приведенной ниже, находится значение l(n)
| Длина ряда n | N 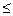 26
| 26<N<153 | 153<n<170 |
| Значение l (n) |
5. Если нарушается хотя бы одно из следующих неравенств, то гипотеза об отсутствии тренда отвергается с доверительной вероятностью 0,95
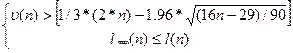
Квадратные скобки неравенства означают целую часть числа.
Пример
Дана динамика ежеквартального выпуска продукции фирмы в ден.ед. С помощью критерия «восходящих и нисходящих» серий сделать вывод о присутствии или отсутствии тренда. Доверительную вероятность принять равной 0,95
|
|
|
| t | ||||||||||||||||
| y1 |
Решение.
Определим последовательность знаков
| t | ||||||||||||||||
| y1 | ||||||||||||||||
| + | - | + | - | + | - | + | - | - | + | + | + | - | + | + |
Число серий
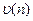= 11, продолжительность самой длинной серии 
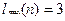, по таблице l(n)=5. Запишем систему неравенств:
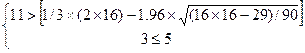
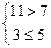
Оба неравенства выполняются, поэтому тренд в динамике выпуска продукции отсутствует с доверительной вероятностью 0,95
