Метод разложения на множители. Метод заключается в использовании разложения на множители данного уравнения

Метод заключается в использовании разложения на множители данного уравнения.

Задача 1. Решите уравнение .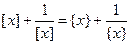

Решение. Преобразуем уравнение: , , , .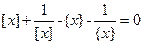

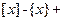
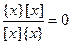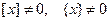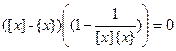Поскольку 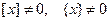, полученное уравнение равносильно уравнению: .

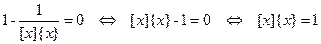Из последнего уравнения следует, что 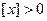, так как дробная часть числа 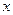больше 0.

Итак, 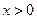. Пусть 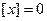(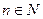), тогда при 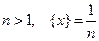. По определению целой части числа 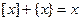, значит, .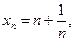

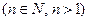Ответ: .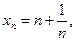

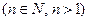Задача 2. Решите уравнение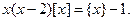

Решение. После преобразований получаем 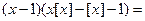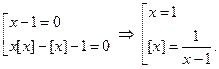Решая графически второе уравнение последней совокупности, убеждаемся, что оно не имеет решений.

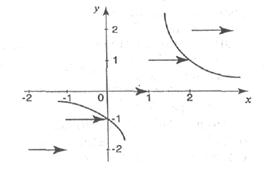
Ответ: 1.

Творческое задание: Сконструировать задачи с целой и дробной частью, решаемые применением метода разложения на множители.