Метод заключается в использование свойств функций или построение графиков функций.
Задача 1. Решите уравнение 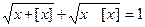 .
.
Решение. Найдем область допустимых значений уравнения:
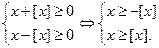
Решением данной системы будут 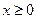 . Рассмотрим два случая:
. Рассмотрим два случая: 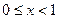 и
и 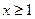 . Если
. Если 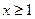 , то
, то 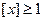 и
и 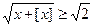 . В этом случае уравнение решений не имеет. Если же
. В этом случае уравнение решений не имеет. Если же 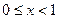 , то
, то 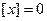 и уравнение принимает вид
и уравнение принимает вид 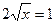 , откуда
, откуда 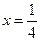 .
.
Ответ: 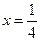 .
.
Задача 2 Решите уравнение 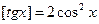 .
.
Решение. Оценим правую часть уравнения 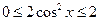 . Значит,
. Значит, 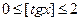 и так как
и так как 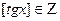 , то
, то 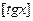 может принимать только значения 0, 1, 2.
может принимать только значения 0, 1, 2.
Рассмотрим три случая.
1. Пусть 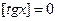 . Тогда из равенства
. Тогда из равенства 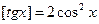 следует, что
следует, что 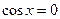 . Функция
. Функция 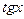 в точках
в точках 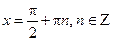 не существует, т.е. при
не существует, т.е. при 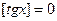 уравнение решений не имеет.
уравнение решений не имеет.
2. Пусть 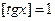 . Тогда
. Тогда 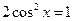 , откуда
, откуда 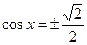 и
и 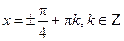 . Так как
. Так как 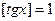 , то из множества решений уравнения
, то из множества решений уравнения 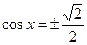 подходит только
подходит только 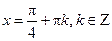 .
.
3. Пусть 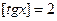 . Тогда
. Тогда 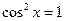 и решениями уравнения являются решения системы
и решениями уравнения являются решения системы 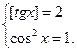
Решив второе уравнение системы, получим 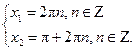
При данных значениях 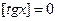 , что противоречит предположению. Следовательно, при
, что противоречит предположению. Следовательно, при 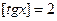 уравнение решений не имеет.
уравнение решений не имеет.
Ответ: 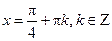 .
.
Задача 3. Решите уравнение 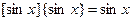 .
.
Решение. Так как область значений функции 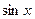 отрезок [-1; 1], то рассмотрим следующие случаи:
отрезок [-1; 1], то рассмотрим следующие случаи:
1. Если 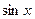 целое число, то
целое число, то 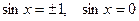 .
.
Так как дробная часть целых чисел равна 0, то 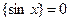 и, следовательно, из значений 1, - 1 и 0 подходит только 0.
и, следовательно, из значений 1, - 1 и 0 подходит только 0. 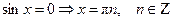 .
.
2. Если 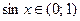 , то
, то 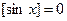 и исходное уравнение примет вид:
и исходное уравнение примет вид: 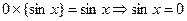 .
.
Но по предположению 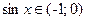 , значит, корней не существует.
, значит, корней не существует.
3. Если 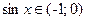 , то
, то 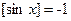
По определению дробной части числа 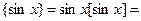
 , и в этом случае уравнение примет вид
, и в этом случае уравнение примет вид 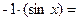
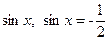 .
.
Полученное значение принадлежит интервалу (-1; 1). Решив уравнение, получим 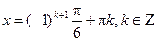 .
.
Ответ: 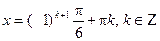 .
.
Задача 4. Решите уравнение 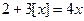 .
.
Решение. Запишем уравнение в виде 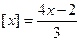 и построим графики функций
и построим графики функций 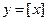 и
и 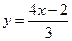 . Эти графики имеют четыре общие:
. Эти графики имеют четыре общие: 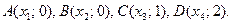 Так как они лежат на прямой, то их координаты удовлетворяют ее уравнению:
Так как они лежат на прямой, то их координаты удовлетворяют ее уравнению: 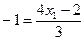 ,
, 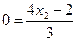 ,
, 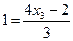 ,
, 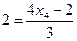 .
.
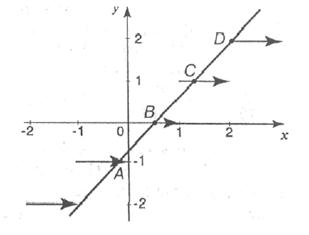
Решая полученные уравнения, находим абсциссы общих точек, которые и будут решениями уравнения.
Ответ: –0,25; 0,5; 1,25; 2.
Творческое задание: Сконструировать задачи с целой и дробной частью, решаемые применением функционально-графического метода.
 2015-02-27
2015-02-27 714
714








