Метод замены переменной. Метод заключается в применении замены выражения определенной переменной (переменными) или замены уравнения смешанной системой с целым параметром р

Метод заключается в применении замены выражения определенной переменной (переменными) или замены уравнения смешанной системой 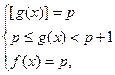с целым параметром р.

Задача 1. Решите уравнение .­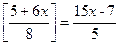

Решение. Произведем замену , .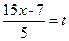

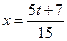Подставим полученное выражение в исходное уравнение 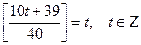. По определению целой части числа .

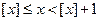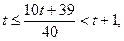
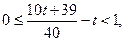
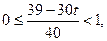
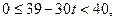
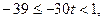
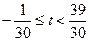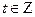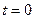. Так как , то или .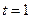

Если 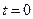, то .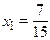

Если 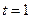, то .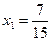

Ответ: .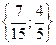

Задача 2. Решите уравнение .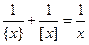

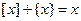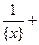
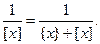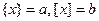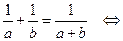
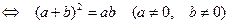
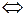
Решение. Так как , то уравнение принимает вид Сделав замену , получим 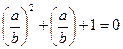. Полученное квадратное уравнение (относительно 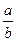) не имеет решений.

Ответ: решений нет.

Задача 3. Решите уравнение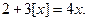

Решение. Рассмотрим систему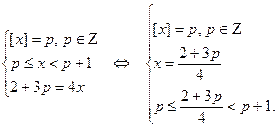

Сначала, решая двойное неравенство, находим те значения параметра 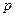, при которых система совместна: 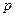=–1, 0, 1, 2, а потом соответствующие значения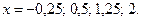

Ответ: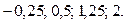

Задача 4. Решите неравенство .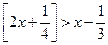

Решение. Обозначим 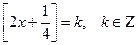. Тогда неравенство примет вид 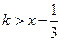. Из определения целой части числа следует .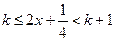

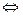
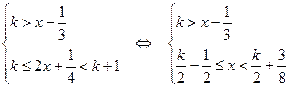Рассмотрим три случая расположения 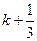на числовой оси.

1) Пусть .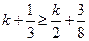

Тогда решениями системы являются .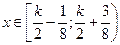

2) Пусть .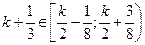

В этом случае решения системы .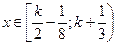

3) Если же 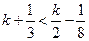, то система решений не имеет.

Итак,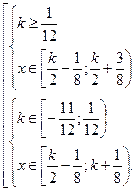

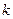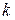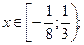Подставим вместо целые значения: при =0 при .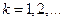

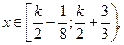
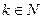Ответ: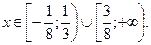

Творческое задание: Сконструировать задачи с целой и дробной частью, решаемые применением метода замены переменной.