Метод перехода

Методы решения уравнений и неравенств

С целой и дробной частью

При решении уравнений и неравенств, содержащих целую и дробную части, можно применить следующие методы:

1. Метод перехода.

2. Функционально-графический метод.

3. Метод разложения на множители.

4. Метод замены переменной.

Метод перехода

Метод заключается в использовании опреде­лений и свойств целой или дробной части числа.

Задача 1. Решите уравнение = .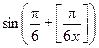

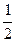Решение. 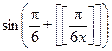= 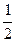- простейшее тригонометрическое уравне­ние. Его решениями будут:

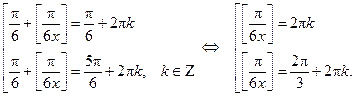
Так как 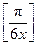принимает только целые значения, а 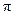- число ирра­циональное, то из двух ра­венств совокупности выполняется только пер­вое при .

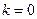Таким образом, 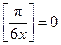и уравнение равносильно двойному нера­венству 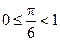. Решая неравенство, получаем .

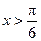Ответ: .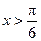

Задача 2. Решите уравнение .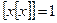

Решение. Так как целая часть левой части уравнения равна 1, то дан­ное уравнение примет вид .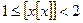

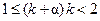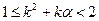Любое число можно представить в виде суммы целой и дробной час­тей, поэтому неравенство мож­но записать в виде или , где .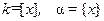

Зная, что 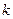принимает целые значения, а 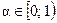, можно сделать вывод, что неравенство (1) верно пр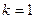и и 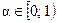, и неверно при , , .

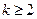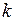
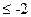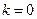При 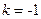неравенство (1) имеет место лишь при .

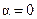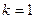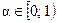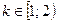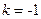Таким образом, неравенство (1) выполняется при и , т.е. при и при и 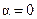, т.е. при .

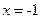Ответ: .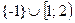

Задача 3. Решите уравнение .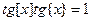

Решение. Так как 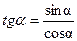, то .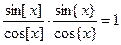

Полученное уравнение равносильно уравнению 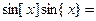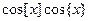, при .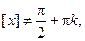

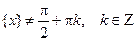По формуле 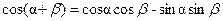получим 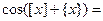0.

Задача 4. Решите неравенство .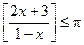

Решение. Если неравенство 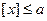справедливо при 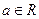, то выполняется неравенство .

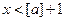Так как 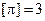, то исходное неравенство равно сильно неравенству .

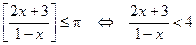Решением последнего неравенства являются .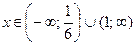

Ответ: .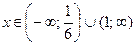

Творческое задание: Сконструировать задачи с целой и дробной частью, решаемые с применением метода перехода.