Лекция 2: Матрицы и определители
1. Операции над матрицами
2. Определители и их свойства
3. Ранг матрицы
4. Обратная матрица. Матричные уравнения
Операции над матрицами
ОПР. Матрицей, размерности 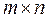 называется прямоугольная таблица чисел
называется прямоугольная таблица чисел
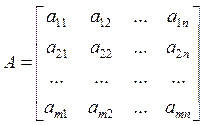 ,
,
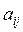 - элемент матрицы,
- элемент матрицы, 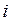 - номер строки,
- номер строки, 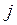 - номер столбца,
- номер столбца, 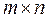 - размерность матрицы.
- размерность матрицы.
ОПР. Нулевой матрицей 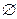 называется матрица, все элементы которой равны нулю, например:
называется матрица, все элементы которой равны нулю, например: 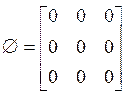 .
.
ОПР. Матрица размерности 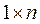 называется матрицей-строкой или просто строкой, например:
называется матрицей-строкой или просто строкой, например: 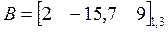 .
.
ОПР. Матрица размерности 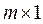 называется матрицей-столбцом или просто столбцом, например:
называется матрицей-столбцом или просто столбцом, например: 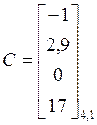 .
.
ОПР. Матрица называется квадратной, если число ее строк равно числу столбцов 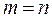 . Число
. Число 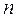 называется порядком матрицы, например при
называется порядком матрицы, например при 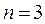 :
:
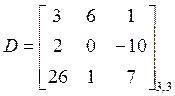 .
.
ОПР. Главной диагональю квадратной матрицы называется диагональ, составленная из чисел 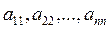 , идущая из левого верхнего угла в правый нижний; побочной называется диагональ, идущая из правого верхнего угла в левый нижний:
, идущая из левого верхнего угла в правый нижний; побочной называется диагональ, идущая из правого верхнего угла в левый нижний:
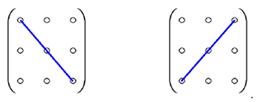
ОПР. Квадратная матрица называется диагональной, если все элементы, стоящие выше и ниже главной диагонали равны нулю, например:
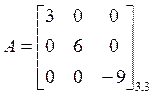 .
.
ОПР. Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали равны нулю, например:
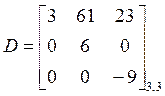 - верхняя треугольная матрица,
- верхняя треугольная матрица,
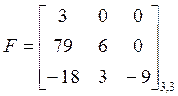 - нижняя треугольная матрица.
- нижняя треугольная матрица.
ОПР. Матрица называется ступенчатой, если все элементы, расположенные ниже главной диагонали равны нулю, например:
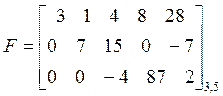 .
.
ОПР. Квадратная матрица с единицами на главной диагонали и нулями выше и ниже ее, называется единичной и обозначается буквой Е, например единичная матрица третьего порядка имеет вид:
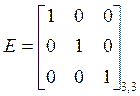 .
.
ОПР. Транспонированием матрицы называется преобразование состоящее в замене строк столбцами с сохранением их номеров, например:
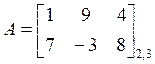 ,
, 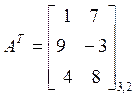 .
.
ОПР. Две матрицы равны 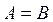 , если равны их размерности и все соответствующие элементы совпадают,
, если равны их размерности и все соответствующие элементы совпадают, 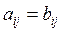 ,
, 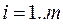 ;
; 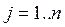 .
.
ОПР. Суммой двух матриц 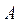 и
и 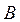 одинаковой размерности
одинаковой размерности 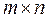 называется матрица
называется матрица 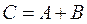 .
.
ПР. Найти сумму матриц 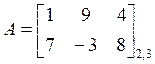 и
и 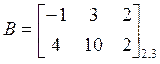 .
.

Свойства операции сложения:
·  ,
,
· 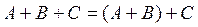 ,
,
· 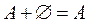 ,
,
· 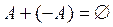 .
.
ОПР. Произведениемматрицы 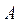 на число
на число 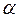 называется матрица
называется матрица 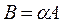 ,
, 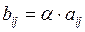 , где
, где 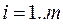 ;
; 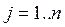 .
.
ПР. Умножить матрицу 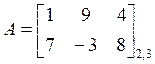 на 3.
на 3.
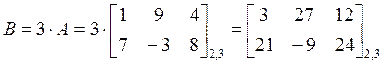 .
.
Свойства операции умножения матрицы на число:
· 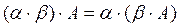 ,
,
· 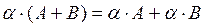 ,
,
· 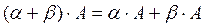 ,
,
· 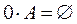 ,
,
· 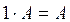
ОПР. Произведениемматриц 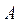 размерности
размерности 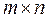 на матрицу
на матрицу 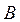 размерности
размерности 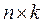 называется матрица
называется матрица 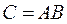 размерности
размерности 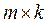 ,элементы которой вычисляются по формуле:
,элементы которой вычисляются по формуле: 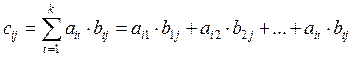 , где
, где 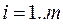 ;
; 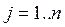 .
.
ЗАМ. Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. 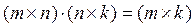 .
.
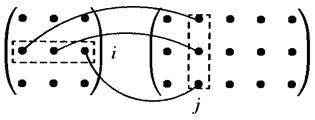
Получение элемента 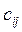 схематично изображается так:
схематично изображается так:
ПР. Найти произведение матриц 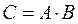
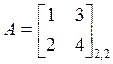 ,
, 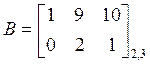 .
.
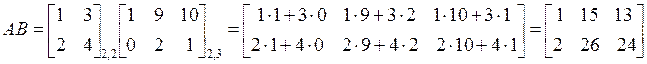
ПР. Найти значение матричного многочлена 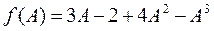 .
.
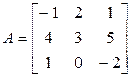 .
.
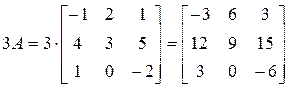 ;
;
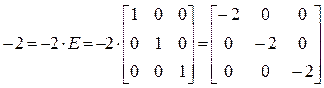 ;
;

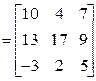 ;
;
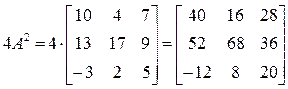 ;
;
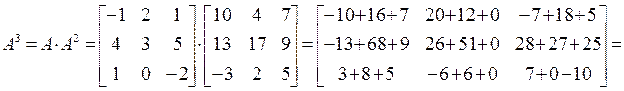
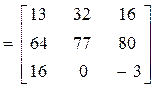 ;
;
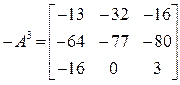 ;
;
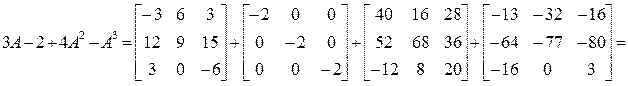
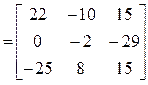 .
.
Свойства операции умножения матриц:
· 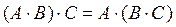 ,
,
· 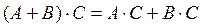 ,
,
·  ,
,
· 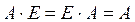 ,
,
· 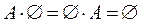 ,
,
· 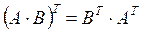 ,
,
ОПР. Матрицы 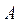 и
и 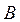 называются перестановочными (коммутирующими), если
называются перестановочными (коммутирующими), если 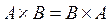 . В общем случае произведение матриц не коммутативно, т.е.
. В общем случае произведение матриц не коммутативно, т.е. 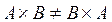 .
.
 2015-02-27
2015-02-27 340
340







