Пусть дано уравнение
f(x)=0 (1.1)
где функция f(x) определена и непрерывна на некотором интервале a<x<b.
Всякое значение ξ 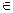 [a,b], обращающее функцию f(x) в нуль, т. е. f(ξ)=0, называется корнем уравнения (1.1) или нулем функции f(x).
[a,b], обращающее функцию f(x) в нуль, т. е. f(ξ)=0, называется корнем уравнения (1.1) или нулем функции f(x).
Если на отрезке [α, β] имеется только один корень, то он называется изолированным корнем.
Теорема о существовании изолированного корня: если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [α, β], т. е. f(α)*f(β)<0, то внутри этого отрезка содержится по крайней мере один корень уравнения f(x)=0, т. е. найдется хотя бы одно число ξ 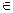 [α, β], такое, что f(ξ)=0.
[α, β], такое, что f(ξ)=0.
Корень заведомо будет единственным, если производная f'(x) существует и сохраняет постоянный знак внутри интервала (α, β), т. е. если f'(x)>0 (если f'(x)<0) при α<x<β.
Процесс отделения корней начинается с установления знаков функций f(x) в граничных точках x= a и x= b интервала a<x<b области существования функции. Затем определяют знаки функции f(x) в ряде промежуточных точек x=x1, x2,.., выбор которых учитывает особенности функции f(x), либо интервал [a, b] делится на равные отрезки [αk<αk+1]. Если окажется, что f(αk)*f(αk+1)<0, то, согласно теоремы, в интервале [αk, αk+1] имеется корень уравнения f(x).
Убедимся, что на отрезке [αk, αk+1] изолированный корень. Рассмотрим несколько способов выявления изолированных корней.
Первый способ. Отрезок [αk, αk+1] делится на две, четыре, восемь и т. д. равных частей, и определяются знаки функции f(x) в точках деления. При этом:
а) если алгебраическое уравнение (1.1) представляет многочлен n-ой степени
a0xn+a1xn-1+…+an=0 (a0 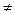 0) (1.2)
0) (1.2)
и произошло n+1 перемен знаков функции на интервале a<x<b, то все корни отделены, т. к. многочлен n-ой степени имеет не более n действительных корней.
Пример. a0x2+a1x+a2=0 – многочлен второй степени.
Выбрав интервал [a, b] рис.1, зададим шаг разбиения h=  , где n- число отрезков [αk, αk+1], где k=0,…,n-1.
, где n- число отрезков [αk, αk+1], где k=0,…,n-1.
 y
y

 f(a) f(b)
f(a) f(b)

 |
a α0 b х
f(α0)
Рис. 1.1

 f(a)>0, f(α0)<0, f(b)>0 – получили три перемены знаков для многочлена второй степени, следовательно на отрезках [a, α0], [α0, b] находятся изолированные корни.
f(a)>0, f(α0)<0, f(b)>0 – получили три перемены знаков для многочлена второй степени, следовательно на отрезках [a, α0], [α0, b] находятся изолированные корни.
б) Если существует непрерывная производная f (x), и корни уравнения f (x)=0 определены, то процесс отделения корней уравнения f(x)=0 можно упорядочить. Для этого достаточно подсчитать лишь знаки функции f(x) в точках нулей ее производной и в граничных точках x= a, и x= b (Рисунок 1.2).
 y
y
 |

 f(x) f'(x3)=0
f(x) f'(x3)=0
 |
x0 x1 x2 x3 х
Рис. 1.2
Второй способ – графическое отделение корней:
действительные корни уравнения f(x)=0 приближенно определяются как абсциссы точек пересечения графика функции y= f(x) с осью x. Если f(x) состоит из простых функций, то уравнение f(x)=0 заменяют равносильным уравнением φ(x)= ψ(x). Тогда, построив графики функций y=φ(x) и y=ψ(x), искомые корни получим как абсциссы точек пересечения этих графиков.
Пример.
Дано уравнение x*lgx-1=0.
графическим способом отделить корни данного уравнения.
1 способ. Строим график функции y=x*lgx-1;
 y -f(x)
y -f(x)



 x
x
1 2 3
Рис.1.3
Выбираем отрезок с изолированным корнем – [2, 3].
2 способ. Уравнение f(x)=0 приведем к виду φ(x)=ψ(x): lgx= 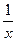 , где φ(x)=lgx, ψ(x)=
, где φ(x)=lgx, ψ(x)= 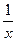 , построим графики y=lg(x), y=
, построим графики y=lg(x), y= 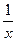 .
.


 y y=
y y= 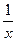 y=lgx
y=lgx
 |
1 2 ξ 3 х
Рис. 1.4- Отрезок с изолированным корнем [2, 3].
 2015-02-27
2015-02-27 2111
2111
