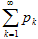Достаточные признаки равномерной сходимости функциональных рядов

Определение 1. Числовой ряд называется мажорантным (или

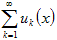мажорирующим) для функционального ряда на множестве X, если " n, " x Î X,

| un (x)|≤ pn.

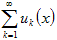Теорема 3. Признак Вейерштрасса. Если для функционального ряда

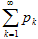на множестве Х существует мажорантный сходящийся числовой ряд, то

исходный функциональный ряд сходится равномерно на множестве Х.

Определение 2. Функциональная последовательность { fn (x)} называется равномерно ограниченной на множестве Х, если существует константа M такая, что " n, " x Î X:

| fn (x)| ≤ M.

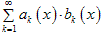Теорема 4. Признак Дирихле-Абеля. Рассмотрим ряд.

1. Пусть функциональная последовательность { bn (x)} не возрастает при каждом x Î X и сходится к нулю равномерно на множестве X (т.е. bn+1 (x) ≤ bn (x) " x Î X, а также bn (x)монотонностремится к нулю при n → ∞ на множестве X).

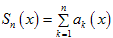2. Последовательность равномерно ограничена на множестве X

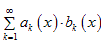Тогда ряд сходится равномерно на множестве X.

ГЛАВА XIX. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ. § 2