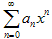Понятие степенного ряда

Теорема 1. Если степенной ряд сходится при x = x 1, то он сходится и притом абсолютно для всех | x | < | x 1|.

Следствие. Если при x = x 1ряд расходится, то он расходится для всех | x | > | x 1|.

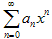Теорема 2. Если степенной ряд сходится для положительного значения x =

x 1, то он сходится равномерно в любом промежутке внутри (−| x 1|; | x 1|).

Рассмотрим последовательность

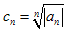(2)

Теорема 3 (Коши-Адамара). Если последовательность (2) не ограничена, то степенной ряд (1) сходится лишь при x = 0.

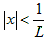Если последовательность (2) ограничена и имеет верхний предел L > 0, то ряд (1)

абсолютно сходится для значений x, удовлетворяющих неравенству и

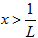расходится для значений x, удовлетворяющих неравенству.

Если последовательность (2) ограничена и её верхний предел L = 0, то ряд (1) сходится абсолютно для всех значений x Î R.

Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что | x | < R ряд абсолютно сходится, а при всех | x | > R ряд расходится.

Определение. Число R называется радиусом сходимости. Интервал (− R, R) назовем областью сходимости.

Отметим, что множество точек, принадлежащее области сходимости, может быть как замкнутым с одной или двух сторон, так и не замкнутым.

Радиус сходимости может быть найден по формуле:

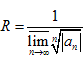
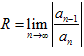или по формуле.

Согласно теореме 2, каково бы ни было положительное число r, удовлетворяющее условию r < R, ряд (1) равномерно сходится на сегменте [− r, r ].

Теорема 4. Непрерывность суммы степенного ряда. Сумма степенного ряда внутри его промежутка сходимости является непрерывной функцией.

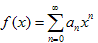Теорема 5. Интегрирование степенных рядов. Если некоторая функция f

(x) определяется степенным рядом:, то для всех x, удовлетворяющих

условию | x | < R, интеграл от этой функции можно записать в виде ряда:

,

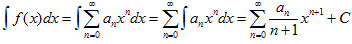то есть степенной ряд можно интегрировать почленно. Последний ряд имеет тот же радиус сходимости, что и исходный.

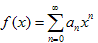Теорема 6. Дифференцирование степенных рядов. Если некоторая функция

f (x) определяется степенным рядом:, то для всех x, удовлетворяющих

условию | x | < R, её производная находится по формуле:

,

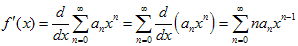то есть ряд можно дифференцировать почленно. Последний ряд имеет тот же радиус сходимости, что и исходный.

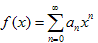2. Сложение, вычитание, умножение и деление степенных рядов. Пусть R 1− радиус

сходимости степенного ряда, а R 2− радиус сходимости степенного ряда

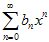. Обозначим R = min (R 1, R 2).

Сложение и вычитание степенных рядов при всех x, удовлетворяющих условию | x | < R, сводится к соответствующим операциям с их членами:

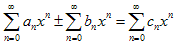, где cn = an ± bn.

Произведение двух степенных рядов при всех x, удовлетворяющих условию | x | < R, выражается формулой:

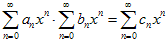Коэффициенты сi находятся по формуле:

сn = a 0 bn + a 1 bn −1+ … + an −1 b 1+ anb 0

Деление двух степенных рядов при всех x, удовлетворяющих условию | x | < R, выражается формулой:

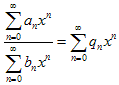
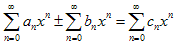Для определения коэффициентов qn рассматриваем произведение

, полученное из записанного выше равенства, и решаем

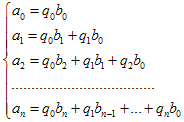систему уравнений:

ГЛАВА XIX. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ. § 4