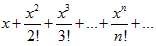Примеры решения задач. 1.Найти область сходимости ряда

1. Найти область сходимости ряда

Решение. Находим радиус сходимости

.

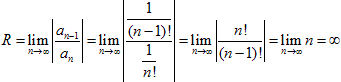Следовательно, данный ряд сходится при любом значении х.

2. Найти область сходимости ряда

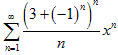(1)

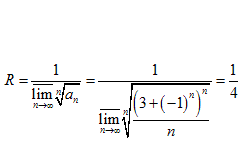Решение. Находим радиус сходимости.

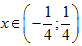Следовательно, данный ряд сходится при.

Исследуем поведение ряда в граничных точках интервала сходимости.

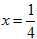Сначала рассмотрим точку. Частичная сумма ряда в этой точке равна

.

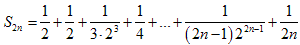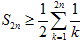Очевидно,. Поскольку последовательность частичных сумм

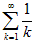гармонического ряда расходится, то, согласно признаку сравнения,

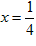последовательность { S 2 n } тоже расходится.

Значит, ряд (1) расходится при

Теперь рассмотрим точку

.

. Частична сумма ряда в этой точке равна

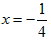
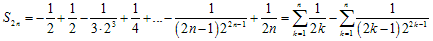
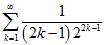Ряд сходится, поэтому сходится и последовательность его частичных

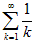сумм. Гармонический ряд расходится.

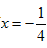Таким образом, последовательность { S 2 n } представляет собой сумму сходящейся и расходящейся последовательности, значит { S 2 n } расходится, а ряд (1) расходится при

.

3. Применяя почленное дифференцирование вычислить сумму ряда

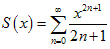(2)

Решение. Сначала определим радиус сходимости числового ряда (2)

.

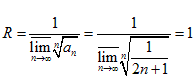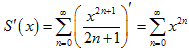Согласно теореме о дифференцировании степенного ряда, при | x | < 1 имеет место

формула.

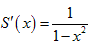Применяя формулу суммы бесконечной геометрической прогрессии при | x | < 1,

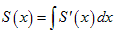получаем:. Вычислим. Для однозначного определения

константы интегрирования, воспользуемся значением S (0) = 0.

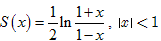Окончательно получим:.

4. Разложение в степенной ряд при помощи формулы Маклорена.

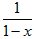Решение. Разложить в ряд функцию.

По формуле Маклорена

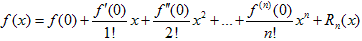, где

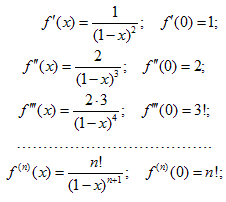Окончательно, получим ряд: f (x) = 1 + x + x 2+ … + xn + …

Рассмотрим способ разложения функции в ряд при помощи интегрирования.

С помощью интегрирования можно разлагать в ряд такую функцию, для которой известно или может быть легко найдено разложение в ряд ее производной.

Находим дифференциал функции df (x) = f ' (x) dx и интегрируем его в пределах от 0 до х.

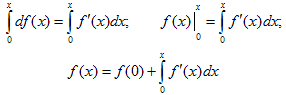
5. Разложитьвряд функцию f (x) = ln(1 + x).

Решение. Решим эту задачу при помощи интегрирования.

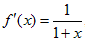Так как, f (0) = 0,

получаем по приведенной выше формуле:

.

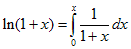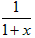Разложение в ряд функции можно получить, если рассматривать эту выражение

как сумму бесконечной геометрической прогрессии со знаменателем − x где | x | < 1:

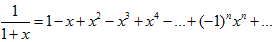Тогда получаем:

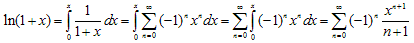
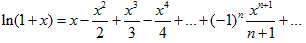Окончательно получим:

ГЛАВА XIX. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ. § 4