Из уравнения (6) следует, что 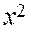
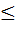
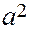 , т. е. – a
, т. е. – a 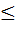 x
x 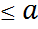 , и
, и
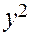
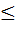
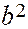 , т. е. – b
, т. е. – b 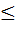 y
y 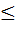 b.
b.
Это означает, что эллипс целиком расположен в прямоугольнике с основанием 2 а и высотой 2 b, а его центр находится в начале координат.
Поскольку в уравнение (8) х и у входят только во второй степени, то эллипс симметричен относительно координатных осей ОУ и ОХ. Для эллипса, описываемого уравнением (8), начало координат является центром симметрии.
Разрешив уравнение (8) относительно у, получим
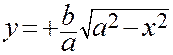 (9)
(9)
и 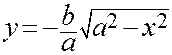 (10).
(10).
Уравнение (9) определяет верхнюю (выше оси ОХ) половину эллипса, а уравнение (10) определяет его нижнюю (ниже оси ОХ) половину.
Точки пересечения эллипса с координатными осями называются его вершинами: верхней – (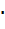 )В1(0; b), нижней – (
)В1(0; b), нижней – (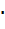 )В2(0;– b), левой –(
)В2(0;– b), левой –(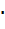 )А1(– a;0) и правой – (
)А1(– a;0) и правой – (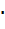 )А2(+ a;0).
)А2(+ a;0).
Отрезки А1А2 и В1В2 называются осями, а отрезки А1О, ОВ1, ОА2, В2О – полуосями эллипса. В случае, когда фокусы расположены на оси ОХ и a 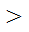 b, отрезок ОА = a называют большой полуосью, а отрезок ОВ = b – малой полуосью.
b, отрезок ОА = a называют большой полуосью, а отрезок ОВ = b – малой полуосью.
При a = b = r уравнение (8) принимает вид
х 2 + у 2 = r 2 (11).
Это соответствует окружности радиуса r с центром в начале координат.
Если параллельным переносом центр эллипса (8) переместить в ( )М0(х 0; у 0), то его уравнение примет вид
)М0(х 0; у 0), то его уравнение примет вид
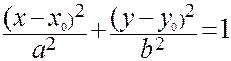 (12).
(12).
Уравнение окружности радиуса r с центром в ( )М0(х 0; у 0) будет иметь вид
)М0(х 0; у 0) будет иметь вид
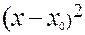 +
+ 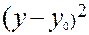 = r 2 (13)
= r 2 (13)
 2015-02-04
2015-02-04 1690
1690
