Определение: Гиперболой[6] называется множество точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек (фокусов[7]), лежащих в этой же плоскости, есть величина постоянная.
Обозначим эту постоянную как 2 а, а расстояние между фокусами F1 и F2 как 2 с (фокусное расстояние), причём a 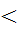 c.
c.
Построим декартову прямоугольную систему координат таким образом, чтобы ось ОХ проходила через фокусы, а её положительное направление совпадало с направлением вектора 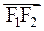 . Начало координатной системы разместим в центре отрезка
. Начало координатной системы разместим в центре отрезка 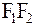 . Тогда координаты фокусов будут иметь вид
. Тогда координаты фокусов будут иметь вид 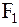 (– с;0) и
(– с;0) и
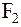 (с;0).
(с;0).
Пусть М (х; у) – произвольная точка гиперболы, тогда



 F1 M – F2 M = 2 a (23).
F1 M – F2 M = 2 a (23).



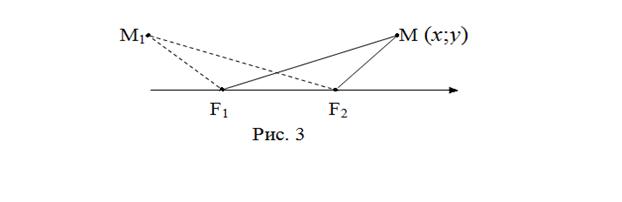
 F1 M =
F1 M = 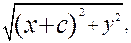 F2 M =
F2 M = 
Тогда уравнение гиперболы принимает вид
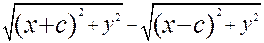
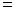
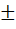 2 a (24).
2 a (24).
Знак «–» в правой части выражения (24) получается в том случае, когда в левой части равенства уменьшаемое оказывается меньше вычитаемого.
После упрощений, подобных тем, что делались в §1, получим
каноническое уравнение гиперболы
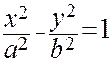 (25),
(25),
где 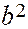
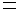 с2–
с2– 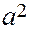 (26).
(26).
 2015-02-04
2015-02-04 1659
1659








