Это простейший тип движения — свободное движение

Первый этап — определение типа движения.

Второй этап — физическая формулировка задачи: выбор системы отсчета, определение действующих сил и начальных условий.

Третий этап — математическая формулировка задачи: запись уравнений,

Это дифференциальное уравнение 2-го порядка.

Записанное для одномерного случая при F = 0, имеет вид

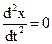
d²x/dt² = 0;

При заданных начальных условиях имеем задачу Коши:

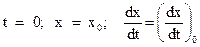
t = 0; x = x₀; dx/dt = (dx/dt)₀;

тогда задача, описываемая этим уравнением, считается корректной.

(Данным уравнением мы можем описать прямолинейное движение.

для совокупности частиц(для каждой)

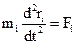
m_id²r_i /dt² = F_i;

из решения этой задачи - определяется положение частиц(координата x).

Таким образом, приближая молекулу к точке, можем фиксировать поведение газа, состоящего из молекул;)

Для одной частицы имеем:

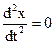
d²x/dt²= 0,

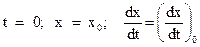
t = 0, x=x₀, dx/dt = (dx/dt)₀;

Четвертый этап — математическое решение задачи.

Решение –интегрирование однородного ОДУ

делается замена ® dx/dt = v

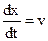
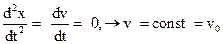
d²x/dt² = dv/dt = 0, ® v = const = v₀

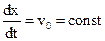
dx/dt = v₀ = const

– уравнение с разделяющимися переменными.

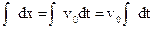
òdx = òv₀ dt = v₀ ò dt

После интегрирования

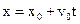
x= x₀ + v₀t

Пятый этап — проверка полученного решения.