Если точка вращается вокруг неподвижной оси, то она описывает окружность с центром на оси вращения, а плоскость этой окружности перпендикулярна оси вращения. Быстроту и направление вращения характеризуют угловой скоростью 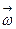 , равной первой производной от углового перемещения
, равной первой производной от углового перемещения 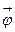 по времени:
по времени: 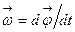 . Вектор угловой скорости
. Вектор угловой скорости 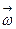 (так же как и вектор углового перемещения d
(так же как и вектор углового перемещения d 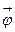 ) перпендикулярен плоскости окружности, по которой движется точка, направлен по оси вращения и связан с направлением вращения правилом
) перпендикулярен плоскости окружности, по которой движется точка, направлен по оси вращения и связан с направлением вращения правилом
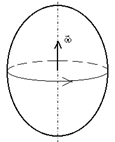
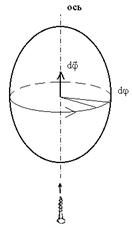 правого винта. Тогда векторы угловой
правого винта. Тогда векторы угловой 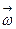 и линейной
и линейной 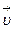 скоростей связаны соотношением:
скоростей связаны соотношением: 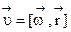 , где
, где 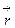 –радиус-вектор движущейся точки, а квадратные скобки означают векторное произведение. Модуль вектора линейной скорости υ=ω· rA, где rA – радиус окружности, по которой движется эта точка.
–радиус-вектор движущейся точки, а квадратные скобки означают векторное произведение. Модуль вектора линейной скорости υ=ω· rA, где rA – радиус окружности, по которой движется эта точка.
Для характеристики неравномерного движения по окружности используется векторная величина, называемая угловым ускорением 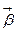 иопределяемая соотношением:
иопределяемая соотношением:
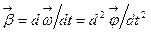 .
.
Если движение материальной точки ускоренное, то векторы угловой скорости и углового ускорения совпадают по направлению; если движение замедленное, то эти векторы направлены в противоположные стороны. Такие векторы, направление которых совпадает с направлением некоторой оси, называются аксиальными. У них нет определенной точки приложения, они могут изображаться в любом месте на оси вращения.
При равнопеременном вращении для величин угловой скорости и углового ускорения выполняются соотношения (аналогичные соотношениям для линейной скорости и линейного ускорения):
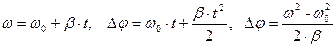 .
.
 2015-02-04
2015-02-04 1443
1443








