Законы сохранения в механике

Любое тело или совокупность тел можно рас­сматривать как систему материальных то­чек. Состояние системы характеризуется зада­нием координат и импульсов всех ее частей. Зная законы действующих в системе сил и со­стояние системы в начальный момент, можно с помощью дифференциальных уравнений ди­намики определить состояние системы в любой момент времени. Но часто ввиду сложности систем и процессов, происходящих в них, не­возможно до конца провести подобное решение.

В системе взаимодействующих тел координаты, скорости и ускорения тел постоянно меняются. Однако, существуют три физические величины, которые в замкнутой системе (системе не взаимодействующей с внешними телами) остаются неизменными (сохра­няются). Такими величинами являются импульс, энергия и мо­мент импульса (об этой величине ниже). Особенно важная роль этих ве­личин связана с тем, что они являются адди­тивными: их значения для системы, состоящей из частей, равно сумме значений для каждой из частей в отдельности.

Закон сохранения механической энер­гии: в инерциальной системе отсчета полная механическая энергия замкнутой системы час­тиц, в которой действуют только консервативные силы, сохраня­ется:

E = Е_КИН + Е_ПОТ = const.

Сохраняется именно полная механическая энергия, в то время как кинетическая и потенци­альная энергии по отдельности могут меняться. В основе закона сохранения механической энергии лежит свойство однородности времени, которое проявляется в том, что физические свойства и законы движения замкнутой системы не зависят от выбора начала отсчета времени. Например, потенциальная энергия поднятого на некоторую высоту тела не меняется с течением времени. Если бы это было не так, то можно было бы поднять тело, дождаться момента, когда его энергия увеличится, и заставить тело совершить работу. Мы получили бы вечный двигатель, работающий за счет разности энергий: возросшей с течением времени и затраченной на подъем тела.

Закон сохранения импульса: в инерциаль­ной системе отсчета импульс замкнутой системы частиц остается постоянным как по величи­не, так и по направлению, т.е. .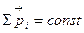

Действительно, из уравнения движения 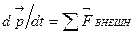следует для замкнутой системы (), что импульс системы 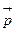остается постоянным.

При этом импульсы отдельных частей систе­мы могут меняться. У незамкнутой системы может сохраняться не сам импульс, а его про­екция на то направление, по которому сумма проекций действующих сил равна нулю. В основе закона сохранения импульса лежит свойство однородности пространства, которое проявляется в том, что физические свойства и законы движения замкнутой системы не зависят от выбора положения начала координат. Если бы пространство было неоднородным, т.е. точки пространства были бы неэквивалентны, то при движении свободного тела эта неэквивалентность проявилась бы в изменении импульса (появлении ускорения).

С помощью законов сохранения можно, не решая уравнений динамики, сделать во многих случаях ряд заключений о свойствах процессов, не вникая в их детальное рассмотрение.

Законы сохранения представляют собой об­щие фундаментальные принципы и отражают свойства пространства и времени.