Центр масс. Закон движения центра масс

В любой совокупности материальных частиц имеется одна точка С, обладающая рядом важ­ных свойств. Эта точка называется центром масс, или центром инерции, а ее положение относительно произвольно выбранного начала отсчета О определяется радиус-вектором 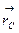: 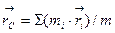, где m_i и 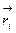– масса и радиус-вектор i -й частицы, 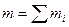– масса всей системы, а суммирование ведется по всем частицам системы.

Точка, определяемая радиус-вектором 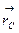, может не совпадать ни с одной из материальных точек, об­разующих систему. Например, у однородного кольца центр масс лежит в его геометрическом центре. У однородных симметричных тел (шар, диск, параллелепи­пед) центр масс совпадает с центром симмет­рии.

Скорость центра масс в данной системе от­счета: ,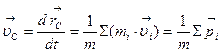

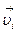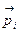где и – скорость и импульс i -й частицы. Отсюда следует, что полный импульс 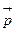системы, равный векторной сумме Σ 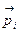импуль­сов частиц, составляющих систему,: 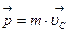, т.е. импульс системы равен произведению мас­сы всей системы на скорость ее центра масс.

Если на систему материальных точек действуют внешние силы 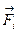, можно записать уравнения их движения: 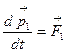; ; 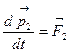··· 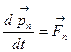. Если сложить эти уравнения, то получим: 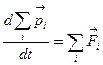. Сделав замены 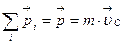и 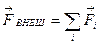получаем уравнение движения системы в виде: .

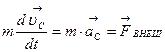Это выражение называется уравнением движе­ния центра масс: при движении любой системы частиц ее центр масс движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены все внешние силы, действующие на систему.

Если сумма внешних сил, действующих на си­стему, равна нулю, то центр масс движется равно­мерно и прямолинейно или покоится. В ИСО таким является случай замкнутой системы. Если 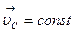, то и полный импульс системы оста­ется неизменным и по величине, и по направлению, т.е. 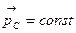. Это означает, что внутренние силы не могут изменить скорость движения центра масс, хотя отдельные части системы могут двигаться относи­тельно друг друга и их импульсы могут изменяться.