Нормальное распределение (рис.12) возникает в том случае, когда результат испытания является следствием влияния большого числа факторов, среди которых нет доминирующих, а объем наблюдений достаточно велик. Это 2-х параметрическое распределение (параметры 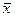 и σ(D)).
и σ(D)).
Для нормального закона распределения общей оценочной характеристикой является дисперсия:
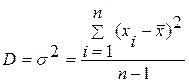
где σ – среднее квадратичное отклонение измеренных значений xi от среднеарифметического 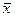 ; n – число измерений.
; n – число измерений.
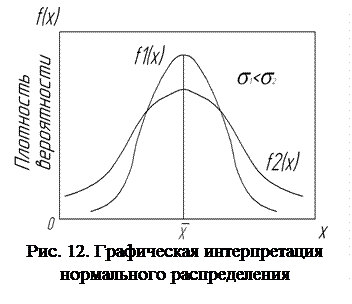 Дисперсия характеризует однородность измерения: чем выше D, тем больше разброс измерений.
Дисперсия характеризует однородность измерения: чем выше D, тем больше разброс измерений.
Плотность распределения вероятностей имеет вид, широко известный как функция Гаусса:

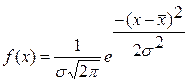
Нормальное распределение применяется для описания отказов, вызванных изнашиванием или постепенным накоплением неисправностей, когда доля внезапных отказов мала, а так же многих других процессов технической эксплуатации автомобилей (периодичность ТО, расход однородных эксплуатационных материалов, рассеяние значений диагностического параметра для исправного состояния, и т.д.). Поскольку он может обрабатывать и отрицательные случайные величины, его широко применяют во многих областях практической и научной деятельности. Закон является симметричным относительно среднего значения. Хотя закон имеет самое большое распространение, его недостатком является сложность выполнения расчетов из-за невозможности непосредственного интегрирования, поэтому для этих целей используется метод, разработанный Лапласом, который ввел подстановку, позволяющую перейти к так называемому центрированному нормированному распределению, имеющему 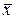 = 0 и σ = 1:
= 0 и σ = 1:
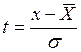 ;
;
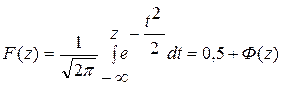 .
.
Показатель вероятности 0,5 соответствует, в силу симметричности нормированного распределения относительно математического ожидания X = 0, значению интеграла в отрицательном диапазоне от - 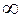 до нуля, который нецелесообразно вычислять. Для положительных аргументов соответствующее значение вероятности находится через интеграл или функцию Лапласа:
до нуля, который нецелесообразно вычислять. Для положительных аргументов соответствующее значение вероятности находится через интеграл или функцию Лапласа:
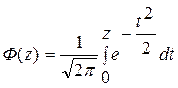 ,
,
Которая была вычислена ее автором через ряд Тейлора и представлена в виде таблицы (см. Приложение 1). При использовании функции Лапласа справедливо соотношение:
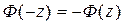
Рассмотрим пример. Фиксировалось время между отказами агрегата автомобиля.
В результате были получены следующие статистические характеристики: 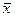 = 36,3 часа; σ = 3,3 часа. Необходимо определить вероятность попадания случайной величины в интервал
= 36,3 часа; σ = 3,3 часа. Необходимо определить вероятность попадания случайной величины в интервал 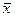 ± 5 часов.
± 5 часов.
Решение задачи сводится к следующему.
Определяется нормированное значение случайной величины в крайних точках интервала
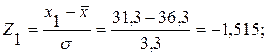
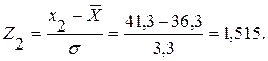
По таблице приложения 1 определяются значения функции Лапласа в граничных точках интервала:
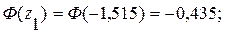
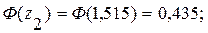
Определяются значения функции распределения в граничных точках интервала:
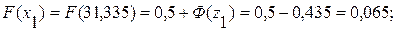
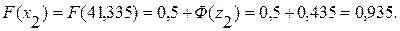
Определяется вероятность попадания случайной величины в интервал X ± 5:
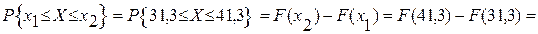
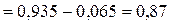
или
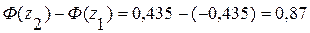 .
.
 2015-02-04
2015-02-04 1098
1098
