Интегральная функция, или более употребительное выражение - функция распределения случайной величины F(x), является наиболее важной, поскольку в основном используется при статистических расчетах, при ее использовании нет необходимости определять площади, а искомые показатели находят по оси ординат.
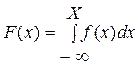
Для ее построения по оси абсцисс откладывают в масштабе значения случайной величины, а по оси ординат накопленную опытную вероятность 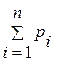
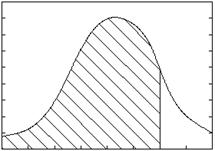
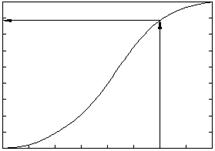
Рис. 11. Графическая интерпретация процесса обработки непрерывной случайной величины при использовании дифференциальной и интегральной функции распределения.
Интегральная функция F(x) имеет следующие свойства:
1. 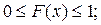
2. 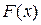 – возрастающая функция, т.е.
– возрастающая функция, т.е. 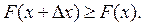
3. При X = – ∞ 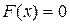 , а при X = + ∞
, а при X = + ∞ 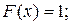
4. Вероятность того, что значение случайной величины X заключено в интервале x и x + ∆x, обычно определяется через функцию F(x):
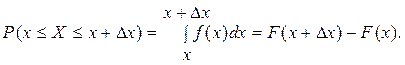
 2015-02-04
2015-02-04 1197
1197
