Задача Д3

Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3–6, прикрепленных к этим нитям, и невесомого блока (рис. Д3.0–Д3.9, табл. Д3).

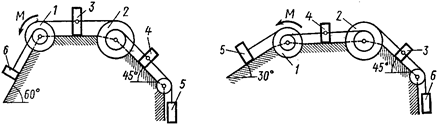
Рис. Д3.0 Рис. Д3.1

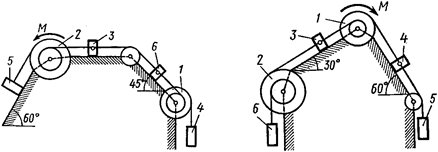
Рис. Д3.2 Рис. Д3.3

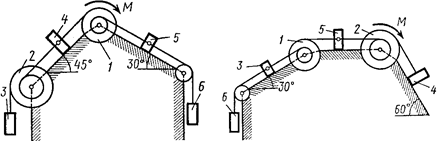
Рис. Д3.4 Рис. Д3.5

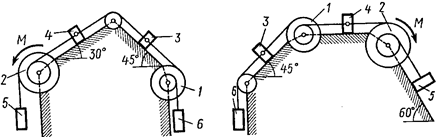
Рис. Д3.6 Рис. Д3.7

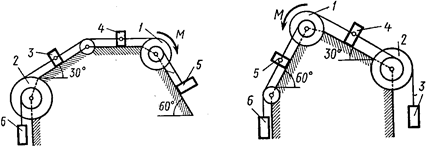
Рис. Д3.8 Рис. Д3.9

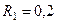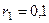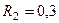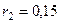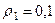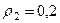Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом , приложенной к одному из шкивов. Радиусы ступеней шкива 1 равны: м, м, шкива 2 – м, м; их радиусы инерции относительно осей вращения равны соответственно м и м.

Пренебрегая трением, найти ускорение тела, имеющего больший вес; веса 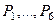шкивов и грузов заданы в таблице. Грузы, веса которых равны нулю, на чертеже можно не изображать (шкивы 1, 2 изображать всегда как части системы).

Таблица Д3

Номер условия							,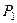

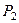
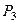
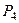
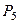
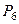
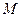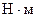
Указания. Задача Д3 – на применение к изучению движения системы уравнений Лагранжа. В задаче система имеет одну степень свободы, ее положение определяется одной обобщенной координатой и для нее должно быть составлено одно уравнение движения. В задачах, где требуется найти ускорение груза 3 (4, 5 или 6), за обобщенную координату удобно принять координату 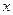, характеризующую перемещение этого груза. Для составления уравнения Лагранжа необходимо найти кинетическую энергию 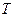системы и выразить все входящие в нее скорости через обобщенную скорость 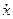, а затем вычислить обобщенную силу 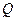. Для этого надо сообщить системе возможное (малое) перемещение, при котором выбранная координата 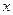получит приращение 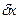, и составить уравнение работ всех сил на этом перемещении. Коэффициент при 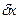в выражении элементарной работы и будет искомой обобщенной силой. Дальнейший ход решения задачи разъяснен в примере Д3.