Теорема 1 (теорема суммы несовместных событий). Вероятность наступления одного из двух несовместных событий (безразлично какого) равна сумме вероятностей этих событий:
Р (А + В) = Р (А) + Р (В).
Следствие 1. Вероятность наступления одного из нескольких попарно несовместных событий (безразлично какого) равна сумме вероятностей этих событий:
Р (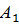 +
+ 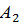 + … +
+ … + 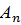 ) = Р (
) = Р (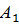 ) + Р (
) + Р (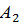 ) + … + Р (
) + … + Р (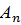 ).
).
Следствие 2. Вероятность события А равна единице минус вероятность его противоположного события Ā:
P (A) = 1 – P (Ā).
Теорема 2 (вероятность суммы совместных событий). Вероятность наступления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного наступления:
P (A + B) = P (A) + P (B) – P (A ∙ B).
Определение 1. Условной вероятностью PA (B) называется вероятность события В при условии, что событие А уже наступило.
Теорема 3 (вероятность произведения двух независимых событий). Вероятность совместного наступления двух независимых событий равна произведению вероятностей этих событий:
P (A ∙ B) = P (A) ∙ P (B).
Следствие 3. Вероятность совместного наступления нескольких независимых событий равна произведению вероятностей этих событий:
P (A 1 · A 2 · … ·An) = P (A 1 ) · P (A 2) · … · P (An).
Теорема 4 (вероятность произведения двух зависимых событий). Вероятность совместного наступления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие наступило:
P (A ∙ B) = P (A) ∙ PA (В).
Следствие 4. Вероятность совместного наступления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причём условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже наступили:
Р (A 1 · A 2 · … ·An)= P (A 1)∙ 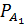 (A 2)∙
(A 2)∙ 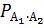 (
(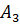 ) ∙ … ∙
) ∙ … ∙ 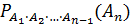 .
.
 2015-02-04
2015-02-04 1211
1211
